pacman::p_load(blorr,corrplot, ggpubr, sf, spdep, GWmodel, tmap, tidyverse, funModeling, skimr, caret)In-Class Exercise 5
First published on 17-Dec-2022
7 Modeling the Spatial Variation of the Explanatory Factors of Water Point Status using Geographically Weighted Logistic Regression
7.1 Overview
In this exercise, we will build an explanatory model to discover factors affecting the water point status of Osun State in Nigeria. Osun is a state in southwestern Nigeria and is named after River Osun - a river which flows through the state. The state was established in Aug-1991 and is made up of 30 Local Government Areas (LGAs).
7.2 The Data
Two pre-processed data sets are used to build the explanatory model. They are:
Osun.rds - it contains LGA boundaries of Osun State. It is in sf polygon data frame, and
Osun_wp_sf.rds - it contains water points within the Osun State. It is in sf point data frame.
7.3 Model Variables
For the Logistic Regression Model that we are building, the following variables on water points are used:
Dependent variable: Water point status:
Class 0: Non-functional water points
Class 1: Functional water points.
Water points with “Unknown” or “NA” status are excluded during pre-processing
Independent variables:
distance_to_primary_road
distance_to_secondary_road
distance_to_tertiary_road
distance_to_city
distance_to_town
water_point_population
local_population_1km
usage_capacity
is_urban
water_source_clean
The first 7 variables are continuous variables while the remaining 3 are discrete variables.
7.4 Getting Started
The following packages are loaded into our R environment for the analysis:
R package for building and validating binary logistic regression models - blorr
R package for calibrating geographical weighted family of models - GWmodel
R package for multivariate data visualisation and analysis - corrplot
Spatial data handling - sf, spdep
Attribute data handling - tidyverse, especially readr, ggplot2 and dplyr
Rapid Exploratory Data Analysis - funModeling
Provide summary statistics about variables in data frames: Skimr, caret
Choropleth mapping - tmap, ggubr
We install and load the relevant packages using the following code chunk.
7.5 Import the data sets in R environment
The LGA boundaries of Osun State are imported and assigned to Osun with the following code chunk.
Osun <- read_rds("In-Class_Ex5/rds/Osun.rds")The water points are imported and assigned to Osun_wp_sf with the following code chunk.
Osun_wp_sf <- read_rds("In-Class_Ex5/rds/Osun_wp_sf.rds")7.6 Exploratory Data Analysis (EDA)
7.6.1 Check the proportion of functional and non-functional water points
We apply the following code to chart the status of water points in Osun
Osun_wp_sf %>% freq(input = 'status')Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as
of ggplot2 3.3.4.
ℹ The deprecated feature was likely used in the funModeling package.
Please report the issue at <https://github.com/pablo14/funModeling/issues>.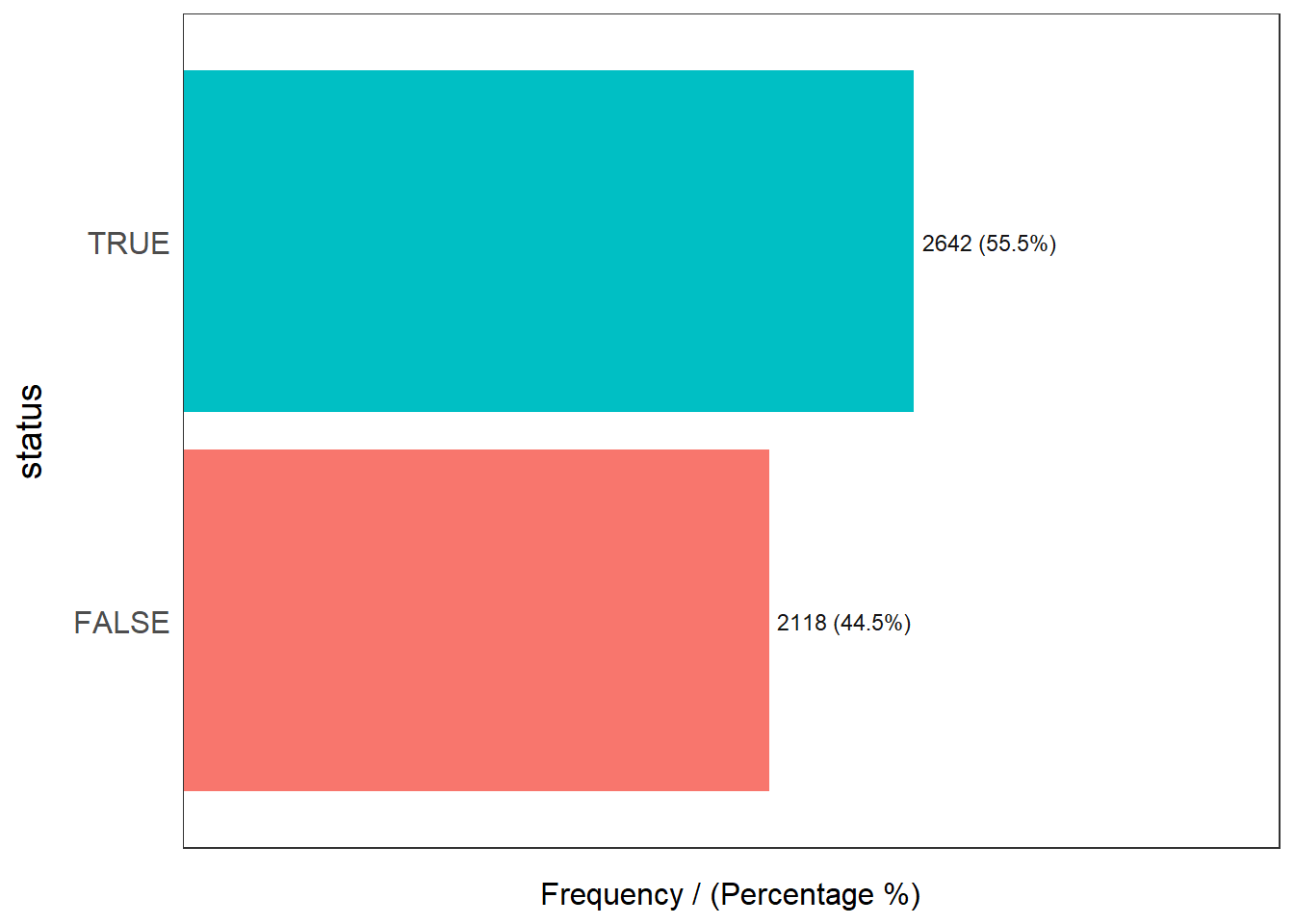
status frequency percentage cumulative_perc
1 TRUE 2642 55.5 55.5
2 FALSE 2118 44.5 100.0We note that the % of non-functional water points is relatively high at 44.5%. At the same time, the proportion of both TRUE (functional) and FALSE (non-functional) classes are relatively balanced.
To visualise where these water points are located in Osun, we plot them by their status on a map using the following code chunk
tmap_mode("view")tmap mode set to interactive viewingactual_status <- tm_shape(Osun)+
#tmap_options(check.and.fix=TRUE)+
tm_polygons(alpha=0.4) +
tm_shape(Osun_wp_sf) +
tm_dots(col='status',
alpha=0.8,
palette = "RdBu") +
tm_view(set.zoom.limits = c(9,12)) +
tm_layout(main.title = "Actual status of Water Points",
main.title.position = "center",
main.title.size = 1.0)
actual_status7.6.2 Inspect the variables for variable type and missing values
We use the skim() of skimr to get summary statistics of all the variables in the water point data frame, Osun_wp_sf .
Osun_wp_sf %>%
skim()Warning: Couldn't find skimmers for class: sfc_POINT, sfc; No user-defined `sfl`
provided. Falling back to `character`.| Name | Piped data |
| Number of rows | 4760 |
| Number of columns | 75 |
| _______________________ | |
| Column type frequency: | |
| character | 47 |
| logical | 5 |
| numeric | 23 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| source | 0 | 1.00 | 5 | 44 | 0 | 2 | 0 |
| report_date | 0 | 1.00 | 22 | 22 | 0 | 42 | 0 |
| status_id | 0 | 1.00 | 2 | 7 | 0 | 3 | 0 |
| water_source_clean | 0 | 1.00 | 8 | 22 | 0 | 3 | 0 |
| water_source_category | 0 | 1.00 | 4 | 6 | 0 | 2 | 0 |
| water_tech_clean | 24 | 0.99 | 9 | 23 | 0 | 3 | 0 |
| water_tech_category | 24 | 0.99 | 9 | 15 | 0 | 2 | 0 |
| facility_type | 0 | 1.00 | 8 | 8 | 0 | 1 | 0 |
| clean_country_name | 0 | 1.00 | 7 | 7 | 0 | 1 | 0 |
| clean_adm1 | 0 | 1.00 | 3 | 5 | 0 | 5 | 0 |
| clean_adm2 | 0 | 1.00 | 3 | 14 | 0 | 35 | 0 |
| clean_adm3 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| clean_adm4 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| installer | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| management_clean | 1573 | 0.67 | 5 | 37 | 0 | 7 | 0 |
| status_clean | 0 | 1.00 | 9 | 32 | 0 | 7 | 0 |
| pay | 0 | 1.00 | 2 | 39 | 0 | 7 | 0 |
| fecal_coliform_presence | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| subjective_quality | 0 | 1.00 | 18 | 20 | 0 | 4 | 0 |
| activity_id | 4757 | 0.00 | 36 | 36 | 0 | 3 | 0 |
| scheme_id | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| wpdx_id | 0 | 1.00 | 12 | 12 | 0 | 4760 | 0 |
| notes | 0 | 1.00 | 2 | 96 | 0 | 3502 | 0 |
| orig_lnk | 4757 | 0.00 | 84 | 84 | 0 | 1 | 0 |
| photo_lnk | 41 | 0.99 | 84 | 84 | 0 | 4719 | 0 |
| country_id | 0 | 1.00 | 2 | 2 | 0 | 1 | 0 |
| data_lnk | 0 | 1.00 | 79 | 96 | 0 | 2 | 0 |
| water_point_history | 0 | 1.00 | 142 | 834 | 0 | 4750 | 0 |
| clean_country_id | 0 | 1.00 | 3 | 3 | 0 | 1 | 0 |
| country_name | 0 | 1.00 | 7 | 7 | 0 | 1 | 0 |
| water_source | 0 | 1.00 | 8 | 30 | 0 | 4 | 0 |
| water_tech | 0 | 1.00 | 5 | 37 | 0 | 20 | 0 |
| adm2 | 0 | 1.00 | 3 | 14 | 0 | 33 | 0 |
| adm3 | 4760 | 0.00 | NA | NA | 0 | 0 | 0 |
| management | 1573 | 0.67 | 5 | 47 | 0 | 7 | 0 |
| adm1 | 0 | 1.00 | 4 | 5 | 0 | 4 | 0 |
| New Georeferenced Column | 0 | 1.00 | 16 | 35 | 0 | 4760 | 0 |
| lat_lon_deg | 0 | 1.00 | 13 | 32 | 0 | 4760 | 0 |
| public_data_source | 0 | 1.00 | 84 | 102 | 0 | 2 | 0 |
| converted | 0 | 1.00 | 53 | 53 | 0 | 1 | 0 |
| created_timestamp | 0 | 1.00 | 22 | 22 | 0 | 2 | 0 |
| updated_timestamp | 0 | 1.00 | 22 | 22 | 0 | 2 | 0 |
| Geometry | 0 | 1.00 | 33 | 37 | 0 | 4760 | 0 |
| ADM2_EN | 0 | 1.00 | 3 | 14 | 0 | 30 | 0 |
| ADM2_PCODE | 0 | 1.00 | 8 | 8 | 0 | 30 | 0 |
| ADM1_EN | 0 | 1.00 | 4 | 4 | 0 | 1 | 0 |
| ADM1_PCODE | 0 | 1.00 | 5 | 5 | 0 | 1 | 0 |
Variable type: logical
| skim_variable | n_missing | complete_rate | mean | count |
|---|---|---|---|---|
| rehab_year | 4760 | 0 | NaN | : |
| rehabilitator | 4760 | 0 | NaN | : |
| is_urban | 0 | 1 | 0.39 | FAL: 2884, TRU: 1876 |
| latest_record | 0 | 1 | 1.00 | TRU: 4760 |
| status | 0 | 1 | 0.56 | TRU: 2642, FAL: 2118 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| row_id | 0 | 1.00 | 68550.48 | 10216.94 | 49601.00 | 66874.75 | 68244.50 | 69562.25 | 471319.00 | ▇▁▁▁▁ |
| lat_deg | 0 | 1.00 | 7.68 | 0.22 | 7.06 | 7.51 | 7.71 | 7.88 | 8.06 | ▁▂▇▇▇ |
| lon_deg | 0 | 1.00 | 4.54 | 0.21 | 4.08 | 4.36 | 4.56 | 4.71 | 5.06 | ▃▆▇▇▂ |
| install_year | 1144 | 0.76 | 2008.63 | 6.04 | 1917.00 | 2006.00 | 2010.00 | 2013.00 | 2015.00 | ▁▁▁▁▇ |
| fecal_coliform_value | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| distance_to_primary_road | 0 | 1.00 | 5021.53 | 5648.34 | 0.01 | 719.36 | 2972.78 | 7314.73 | 26909.86 | ▇▂▁▁▁ |
| distance_to_secondary_road | 0 | 1.00 | 3750.47 | 3938.63 | 0.15 | 460.90 | 2554.25 | 5791.94 | 19559.48 | ▇▃▁▁▁ |
| distance_to_tertiary_road | 0 | 1.00 | 1259.28 | 1680.04 | 0.02 | 121.25 | 521.77 | 1834.42 | 10966.27 | ▇▂▁▁▁ |
| distance_to_city | 0 | 1.00 | 16663.99 | 10960.82 | 53.05 | 7930.75 | 15030.41 | 24255.75 | 47934.34 | ▇▇▆▃▁ |
| distance_to_town | 0 | 1.00 | 16726.59 | 12452.65 | 30.00 | 6876.92 | 12204.53 | 27739.46 | 44020.64 | ▇▅▃▃▂ |
| rehab_priority | 2654 | 0.44 | 489.33 | 1658.81 | 0.00 | 7.00 | 91.50 | 376.25 | 29697.00 | ▇▁▁▁▁ |
| water_point_population | 4 | 1.00 | 513.58 | 1458.92 | 0.00 | 14.00 | 119.00 | 433.25 | 29697.00 | ▇▁▁▁▁ |
| local_population_1km | 4 | 1.00 | 2727.16 | 4189.46 | 0.00 | 176.00 | 1032.00 | 3717.00 | 36118.00 | ▇▁▁▁▁ |
| crucialness_score | 798 | 0.83 | 0.26 | 0.28 | 0.00 | 0.07 | 0.15 | 0.35 | 1.00 | ▇▃▁▁▁ |
| pressure_score | 798 | 0.83 | 1.46 | 4.16 | 0.00 | 0.12 | 0.41 | 1.24 | 93.69 | ▇▁▁▁▁ |
| usage_capacity | 0 | 1.00 | 560.74 | 338.46 | 300.00 | 300.00 | 300.00 | 1000.00 | 1000.00 | ▇▁▁▁▅ |
| days_since_report | 0 | 1.00 | 2692.69 | 41.92 | 1483.00 | 2688.00 | 2693.00 | 2700.00 | 4645.00 | ▁▇▁▁▁ |
| staleness_score | 0 | 1.00 | 42.80 | 0.58 | 23.13 | 42.70 | 42.79 | 42.86 | 62.66 | ▁▁▇▁▁ |
| location_id | 0 | 1.00 | 235865.49 | 6657.60 | 23741.00 | 230638.75 | 236199.50 | 240061.25 | 267454.00 | ▁▁▁▁▇ |
| cluster_size | 0 | 1.00 | 1.05 | 0.25 | 1.00 | 1.00 | 1.00 | 1.00 | 4.00 | ▇▁▁▁▁ |
| lat_deg_original | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| lon_deg_original | 4760 | 0.00 | NaN | NA | NA | NA | NA | NA | NA | |
| count | 0 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ▁▁▇▁▁ |
Things to note in the generated results
A frequency count of the data type of columns - character, logical, numeric - is provided.
Variables with excessive missing values should not be used for linear and logistic regression modeling. For instance, install_year will give us an idea of the age of the water point and presumably older water points tend to be non_functional as compared to the newer ones. However, we don’t use install_year for our model due to the high proportion of missing values (~24% missing) in the column.
Variables with a few missing values and assessed to be useful for the model can be included. We can remove the records with missing values from the data base. For our case, since water_point_population and local_population_1km only have 4 missing records, we will remove the 4 records and include the 2 variables for subsequent analysis. Using the results above, the number of missing values for each selected variable is as follow:
Status - 0 missing
distance_to_primary_road - 0 missing
distance_to_secondary_road - 0 missing
distance_to_tertiary_road - 0 missing
distance_to_city - 0 missing
distance_to_town - 0 missing
water_point_population - 4 missing
local_population_1km - 4 missing
usage_capacity - 0 missing
is_urban - 0 missing
water_source_clean - 0 missing
We use the following code chunk to filter out records with missing values for water_point_population and local_population columns. After running this code, we should observe that the number of records has by 4 from 4,760 to 4,756.
Osun_wp_sf_clean <- Osun_wp_sf %>%
filter_at(vars(water_point_population,
local_population_1km,
),
all_vars(!is.na(.)))- We note that usage_capacity is recognised as a numeric variable in R whereas it is more of a categorical variable denoting the type of water point. We change its data type to factor using the following code. After running this code, we should observe that usage capacity has been changed to “factor” type with 2 levels.
Osun_wp_sf_clean <- Osun_wp_sf_clean %>%
mutate(usage_capacity = as.factor(usage_capacity))7.7 Correlation Analysis
We first extract the selected variables from the Osun_wp_sf_clean and remove the geometry information from the data in order to construct a correlation matrix.
Osun_wp <- Osun_wp_sf_clean %>%
select(c(7,35:39,42:43,46:47,57)) %>%
st_set_geometry(NULL)Then, we plot the matrix for all the numeric variables (excluding the dependent variable).
cluster_vars.cor = cor(
Osun_wp[,2:7])
corrplot.mixed(cluster_vars.cor,
lower = 'ellipse',
upper = "number",
tl.pos = "lt",
diag = "l",
tl.col= "black"
)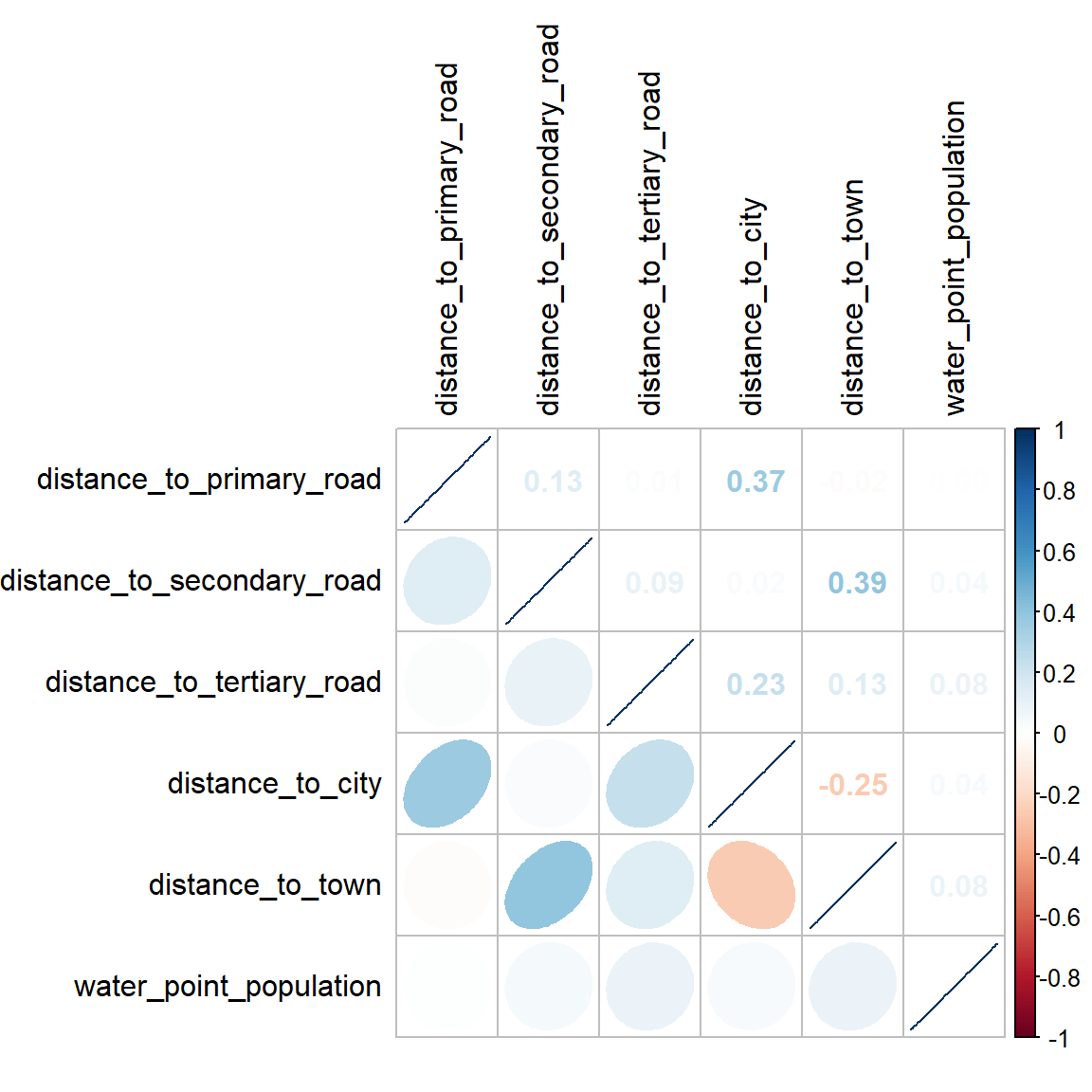
Based on the results above, there is no sign of multicollinearity among the 6 continuous variables since none of the absolute correlation value of the variable pairs is above 0.85. We will go ahead and use all the 6 variables for modelling.
7.8 Build a Global (and non-spatial) Logistic Regression Model
Logistic Regression is a type of Generalised Linear Model (GLM) and we use the glm() of R stats to fit the model.
model <- glm(status ~ distance_to_primary_road +
distance_to_secondary_road +
distance_to_tertiary_road +
distance_to_city +
distance_to_town +
water_point_population +
local_population_1km +
usage_capacity +
is_urban +
water_source_clean,
data = Osun_wp_sf_clean,
family = binomial(link='logit'))Instead of typing Model to view the results, we use the blr_regress() of blorr to produce a more informative report to help us examine the results of the model
blr_regress(model) Model Overview
------------------------------------------------------------------------
Data Set Resp Var Obs. Df. Model Df. Residual Convergence
------------------------------------------------------------------------
data status 4756 4755 4744 TRUE
------------------------------------------------------------------------
Response Summary
--------------------------------------------------------
Outcome Frequency Outcome Frequency
--------------------------------------------------------
0 2114 1 2642
--------------------------------------------------------
Maximum Likelihood Estimates
-----------------------------------------------------------------------------------------------
Parameter DF Estimate Std. Error z value Pr(>|z|)
-----------------------------------------------------------------------------------------------
(Intercept) 1 0.3887 0.1124 3.4588 5e-04
distance_to_primary_road 1 0.0000 0.0000 -0.7153 0.4744
distance_to_secondary_road 1 0.0000 0.0000 -0.5530 0.5802
distance_to_tertiary_road 1 1e-04 0.0000 4.6708 0.0000
distance_to_city 1 0.0000 0.0000 -4.7574 0.0000
distance_to_town 1 0.0000 0.0000 -4.9170 0.0000
water_point_population 1 -5e-04 0.0000 -11.3686 0.0000
local_population_1km 1 3e-04 0.0000 19.2953 0.0000
usage_capacity1000 1 -0.6230 0.0697 -8.9366 0.0000
is_urbanTRUE 1 -0.2971 0.0819 -3.6294 3e-04
water_source_cleanProtected Shallow Well 1 0.5040 0.0857 5.8783 0.0000
water_source_cleanProtected Spring 1 1.2882 0.4388 2.9359 0.0033
-----------------------------------------------------------------------------------------------
Association of Predicted Probabilities and Observed Responses
---------------------------------------------------------------
% Concordant 0.7347 Somers' D 0.4693
% Discordant 0.2653 Gamma 0.4693
% Tied 0.0000 Tau-a 0.2318
Pairs 5585188 c 0.7347
---------------------------------------------------------------Things to note from the report:
distance_to_primary_road and distance_to_secondary_road have p-values that > 0.05, we can remove these 2 variables from our model since they are not statistically significant
For categorical variables, positive Estimate (or coefficient) value implies an above average correlation and a negative value implies below average correlation. The magnitude of the coefficient does not matter for categorical variables;
For continuous variables, positive Estimate value implies direct correlation and a negative Estimate value implies an inverse correlation. The magnitude of the Estimate value provides the strength of the correlation.
To appreciate the performance of the model, we generate the confusion matrix using blr_confusion_matrix() of blorr.
# Probability cut-off threshold for Class 1 is set at 0.5
blr_confusion_matrix(model,cutoff = 0.5)Confusion Matrix and Statistics
Reference
Prediction FALSE TRUE
0 1301 738
1 813 1904
Accuracy : 0.6739
No Information Rate : 0.4445
Kappa : 0.3373
McNemars's Test P-Value : 0.0602
Sensitivity : 0.7207
Specificity : 0.6154
Pos Pred Value : 0.7008
Neg Pred Value : 0.6381
Prevalence : 0.5555
Detection Rate : 0.4003
Detection Prevalence : 0.5713
Balanced Accuracy : 0.6680
Precision : 0.7008
Recall : 0.7207
'Positive' Class : 1The accuracy of the model is 0.6716 is a good start and it is better than a random guess with 0.5 accuracy.
7.9 Build a Geographically Weighted Logistic Regression Model
Now, we take into account the geographic information of the water points in our model.
7.9.1 Convert the water point sf data frame to sp data frame
First, we convert the Osun_wp_sf_clean data frame from sf to sp for GW modelling. This is because GWmodel is a relatively older package which can only work with sp data frames.
Osun_wp_sp <- Osun_wp_sf_clean %>%
select(c(status,
distance_to_primary_road,
distance_to_secondary_road,
distance_to_tertiary_road,
distance_to_city,
distance_to_town,
water_point_population,
local_population_1km,
usage_capacity,
is_urban,
water_source_clean)) %>%
as_Spatial()
Osun_wp_spclass : SpatialPointsDataFrame
features : 4756
extent : 182502.4, 290751, 340054.1, 450905.3 (xmin, xmax, ymin, ymax)
crs : +proj=tmerc +lat_0=4 +lon_0=8.5 +k=0.99975 +x_0=670553.98 +y_0=0 +a=6378249.145 +rf=293.465 +towgs84=-92,-93,122,0,0,0,0 +units=m +no_defs
variables : 11
names : status, distance_to_primary_road, distance_to_secondary_road, distance_to_tertiary_road, distance_to_city, distance_to_town, water_point_population, local_population_1km, usage_capacity, is_urban, water_source_clean
min values : 0, 0.014461356813335, 0.152195902540837, 0.017815121653488, 53.0461399623541, 30.0019777713073, 0, 0, 1000, 0, Borehole
max values : 1, 26909.8616132094, 19559.4793799085, 10966.2705628969, 47934.343603562, 44020.6393368124, 29697, 36118, 300, 1, Protected Spring 7.9.2 Derive a Fixed Bandwidth for the GWLR Model
bw.fixed <- bw.ggwr(status ~ distance_to_primary_road +
distance_to_secondary_road +
distance_to_tertiary_road +
distance_to_city +
distance_to_town +
water_point_population +
local_population_1km +
usage_capacity +
is_urban +
water_source_clean,
data = Osun_wp_sp,
family = "binomial",
approach = "AIC",
kernel = "gaussian",
adaptive = FALSE,
longlat = FALSE)Take a cup of tea and have a break, it will take a few minutes.
-----A kind suggestion from GWmodel development group
Iteration Log-Likelihood:(With bandwidth: 95768.67 )
=========================
0 -2889
1 -2836
2 -2830
3 -2829
4 -2829
5 -2829
Fixed bandwidth: 95768.67 AICc value: 5684.357
Iteration Log-Likelihood:(With bandwidth: 59200.13 )
=========================
0 -2875
1 -2818
2 -2810
3 -2808
4 -2808
5 -2808
Fixed bandwidth: 59200.13 AICc value: 5646.785
Iteration Log-Likelihood:(With bandwidth: 36599.53 )
=========================
0 -2847
1 -2781
2 -2768
3 -2765
4 -2765
5 -2765
6 -2765
Fixed bandwidth: 36599.53 AICc value: 5575.148
Iteration Log-Likelihood:(With bandwidth: 22631.59 )
=========================
0 -2798
1 -2719
2 -2698
3 -2693
4 -2693
5 -2693
6 -2693
Fixed bandwidth: 22631.59 AICc value: 5466.883
Iteration Log-Likelihood:(With bandwidth: 13998.93 )
=========================
0 -2720
1 -2622
2 -2590
3 -2581
4 -2580
5 -2580
6 -2580
7 -2580
Fixed bandwidth: 13998.93 AICc value: 5324.578
Iteration Log-Likelihood:(With bandwidth: 8663.649 )
=========================
0 -2601
1 -2476
2 -2431
3 -2419
4 -2417
5 -2417
6 -2417
7 -2417
Fixed bandwidth: 8663.649 AICc value: 5163.61
Iteration Log-Likelihood:(With bandwidth: 5366.266 )
=========================
0 -2436
1 -2268
2 -2194
3 -2167
4 -2161
5 -2161
6 -2161
7 -2161
8 -2161
9 -2161
Fixed bandwidth: 5366.266 AICc value: 4990.587
Iteration Log-Likelihood:(With bandwidth: 3328.371 )
=========================
0 -2157
1 -1922
2 -1802
3 -1739
4 -1713
5 -1713
Fixed bandwidth: 3328.371 AICc value: 4798.288
Iteration Log-Likelihood:(With bandwidth: 2068.882 )
=========================
0 -1751
1 -1421
2 -1238
3 -1133
4 -1084
5 -1084
Fixed bandwidth: 2068.882 AICc value: 4837.017
Iteration Log-Likelihood:(With bandwidth: 4106.777 )
=========================
0 -2297
1 -2095
2 -1997
3 -1951
4 -1938
5 -1936
6 -1936
7 -1936
8 -1936
Fixed bandwidth: 4106.777 AICc value: 4873.161
Iteration Log-Likelihood:(With bandwidth: 2847.289 )
=========================
0 -2036
1 -1771
2 -1633
3 -1558
4 -1525
5 -1525
Fixed bandwidth: 2847.289 AICc value: 4768.192
Iteration Log-Likelihood:(With bandwidth: 2549.964 )
=========================
0 -1941
1 -1655
2 -1503
3 -1417
4 -1378
5 -1378
Fixed bandwidth: 2549.964 AICc value: 4762.212
Iteration Log-Likelihood:(With bandwidth: 2366.207 )
=========================
0 -1874
1 -1573
2 -1410
3 -1316
4 -1274
5 -1274
Fixed bandwidth: 2366.207 AICc value: 4773.081
Iteration Log-Likelihood:(With bandwidth: 2663.532 )
=========================
0 -1979
1 -1702
2 -1555
3 -1474
4 -1438
5 -1438
Fixed bandwidth: 2663.532 AICc value: 4762.568
Iteration Log-Likelihood:(With bandwidth: 2479.775 )
=========================
0 -1917
1 -1625
2 -1468
3 -1380
4 -1339
5 -1339
Fixed bandwidth: 2479.775 AICc value: 4764.294
Iteration Log-Likelihood:(With bandwidth: 2593.343 )
=========================
0 -1956
1 -1674
2 -1523
3 -1439
4 -1401
5 -1401
Fixed bandwidth: 2593.343 AICc value: 4761.813
Iteration Log-Likelihood:(With bandwidth: 2620.153 )
=========================
0 -1965
1 -1685
2 -1536
3 -1453
4 -1415
5 -1415
Fixed bandwidth: 2620.153 AICc value: 4761.89
Iteration Log-Likelihood:(With bandwidth: 2576.774 )
=========================
0 -1950
1 -1667
2 -1515
3 -1431
4 -1393
5 -1393
Fixed bandwidth: 2576.774 AICc value: 4761.889
Iteration Log-Likelihood:(With bandwidth: 2603.584 )
=========================
0 -1960
1 -1678
2 -1528
3 -1445
4 -1407
5 -1407
Fixed bandwidth: 2603.584 AICc value: 4761.813
Iteration Log-Likelihood:(With bandwidth: 2609.913 )
=========================
0 -1962
1 -1680
2 -1531
3 -1448
4 -1410
5 -1410
Fixed bandwidth: 2609.913 AICc value: 4761.831
Iteration Log-Likelihood:(With bandwidth: 2599.672 )
=========================
0 -1958
1 -1676
2 -1526
3 -1443
4 -1405
5 -1405
Fixed bandwidth: 2599.672 AICc value: 4761.809
Iteration Log-Likelihood:(With bandwidth: 2597.255 )
=========================
0 -1957
1 -1675
2 -1525
3 -1441
4 -1403
5 -1403
Fixed bandwidth: 2597.255 AICc value: 4761.809 # Adaptaive is set to "FALSE" as we are computing fixed width
# longlat is set to "FALSE" as we are using projected CRS (instead of coordinate points)bw.fixed[1] 2599.672The derived bandwidth is 2599.672 metres.
7.9.3 Fit the Fixed Bandwidth and data into the GWLR model
We fit the model using the bandwidth obtained above.
gwlr.fixed <- ggwr.basic(status ~ distance_to_primary_road +
distance_to_secondary_road +
distance_to_tertiary_road +
distance_to_city +
distance_to_town +
water_point_population +
local_population_1km +
usage_capacity +
is_urban +
water_source_clean,
data = Osun_wp_sp,
bw=2599.672,
family = "binomial",
kernel = "gaussian",
adaptive = FALSE,
longlat = FALSE)Warning in proj4string(data): CRS object has comment, which is lost in output; in tests, see
https://cran.r-project.org/web/packages/sp/vignettes/CRS_warnings.htmlWarning in proj4string(regression.points): CRS object has comment, which is lost in output; in tests, see
https://cran.r-project.org/web/packages/sp/vignettes/CRS_warnings.html Iteration Log-Likelihood
=========================
0 -1958
1 -1676
2 -1526
3 -1443
4 -1405
5 -1405 We call the model to view the results
gwlr.fixed ***********************************************************************
* Package GWmodel *
***********************************************************************
Program starts at: 2022-12-18 00:02:04
Call:
ggwr.basic(formula = status ~ distance_to_primary_road + distance_to_secondary_road +
distance_to_tertiary_road + distance_to_city + distance_to_town +
water_point_population + local_population_1km + usage_capacity +
is_urban + water_source_clean, data = Osun_wp_sp, bw = 2599.672,
family = "binomial", kernel = "gaussian", adaptive = FALSE,
longlat = FALSE)
Dependent (y) variable: status
Independent variables: distance_to_primary_road distance_to_secondary_road distance_to_tertiary_road distance_to_city distance_to_town water_point_population local_population_1km usage_capacity is_urban water_source_clean
Number of data points: 4756
Used family: binomial
***********************************************************************
* Results of Generalized linear Regression *
***********************************************************************
Call:
NULL
Deviance Residuals:
Min 1Q Median 3Q Max
-124.555 -1.755 1.072 1.742 34.333
Coefficients:
Estimate Std. Error z value Pr(>|z|)
Intercept 3.887e-01 1.124e-01 3.459 0.000543
distance_to_primary_road -4.642e-06 6.490e-06 -0.715 0.474422
distance_to_secondary_road -5.143e-06 9.299e-06 -0.553 0.580230
distance_to_tertiary_road 9.683e-05 2.073e-05 4.671 3.00e-06
distance_to_city -1.686e-05 3.544e-06 -4.757 1.96e-06
distance_to_town -1.480e-05 3.009e-06 -4.917 8.79e-07
water_point_population -5.097e-04 4.484e-05 -11.369 < 2e-16
local_population_1km 3.451e-04 1.788e-05 19.295 < 2e-16
usage_capacity1000 -6.230e-01 6.972e-02 -8.937 < 2e-16
is_urbanTRUE -2.971e-01 8.185e-02 -3.629 0.000284
water_source_cleanProtected Shallow Well 5.040e-01 8.574e-02 5.878 4.14e-09
water_source_cleanProtected Spring 1.288e+00 4.388e-01 2.936 0.003325
Intercept ***
distance_to_primary_road
distance_to_secondary_road
distance_to_tertiary_road ***
distance_to_city ***
distance_to_town ***
water_point_population ***
local_population_1km ***
usage_capacity1000 ***
is_urbanTRUE ***
water_source_cleanProtected Shallow Well ***
water_source_cleanProtected Spring **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 6534.5 on 4755 degrees of freedom
Residual deviance: 5688.0 on 4744 degrees of freedom
AIC: 5712
Number of Fisher Scoring iterations: 5
AICc: 5712.099
Pseudo R-square value: 0.1295351
***********************************************************************
* Results of Geographically Weighted Regression *
***********************************************************************
*********************Model calibration information*********************
Kernel function: gaussian
Fixed bandwidth: 2599.672
Regression points: the same locations as observations are used.
Distance metric: A distance matrix is specified for this model calibration.
************Summary of Generalized GWR coefficient estimates:**********
Min. 1st Qu. Median
Intercept -8.7229e+02 -4.9955e+00 1.7600e+00
distance_to_primary_road -1.9389e-02 -4.8031e-04 2.9618e-05
distance_to_secondary_road -1.5921e-02 -3.7551e-04 1.2317e-04
distance_to_tertiary_road -1.5618e-02 -4.2368e-04 7.6179e-05
distance_to_city -1.8416e-02 -5.6217e-04 -1.2726e-04
distance_to_town -2.2411e-02 -5.7283e-04 -1.5155e-04
water_point_population -5.2208e-02 -2.2767e-03 -9.8875e-04
local_population_1km -1.2698e-01 4.9952e-04 1.0638e-03
usage_capacity1000 -2.0772e+01 -9.7231e-01 -4.1592e-01
is_urbanTRUE -1.9790e+02 -4.2908e+00 -1.6864e+00
water_source_cleanProtected.Shallow.Well -2.0789e+01 -4.5190e-01 5.3340e-01
water_source_cleanProtected.Spring -5.2235e+02 -5.5977e+00 2.5441e+00
3rd Qu. Max.
Intercept 1.2763e+01 1073.2156
distance_to_primary_road 4.8443e-04 0.0142
distance_to_secondary_road 6.0692e-04 0.0258
distance_to_tertiary_road 6.6815e-04 0.0128
distance_to_city 2.3718e-04 0.0150
distance_to_town 1.9271e-04 0.0224
water_point_population 5.0102e-04 0.1309
local_population_1km 1.8157e-03 0.0392
usage_capacity1000 3.0322e-01 5.9281
is_urbanTRUE 1.2841e+00 744.3099
water_source_cleanProtected.Shallow.Well 1.7849e+00 67.6343
water_source_cleanProtected.Spring 6.7663e+00 317.4133
************************Diagnostic information*************************
Number of data points: 4756
GW Deviance: 2795.084
AIC : 4414.606
AICc : 4747.423
Pseudo R-square value: 0.5722559
***********************************************************************
Program stops at: 2022-12-18 00:02:38 Things to note:
The report above has 2 sections -Global Logistic Regression (Global LR) model and Geographically Weighted Logistic Regression (GWLR) model results.
The Global LR model’s AICc is 5712.099 while the GWLR model’s AICc is 4747.423. This shows that the GWLR model better fit the data than the Global LR.
7.9.4 Model assessment and comparison
To assess the performance of the gwlr, we will convert the SDF object to a data frame by using the code chunk below
gwr.fixed <- as.data.frame(gwlr.fixed$SDF)Next, we label yhat values (probability of water point being functional) greater or equal to 0.5 into 1 or else 0. The result of the logic comparison operation will be saved in a column called most.
gwr.fixed <- gwr.fixed %>%
mutate(most = ifelse(
gwr.fixed$yhat >= 0.5,T,F))Then we construct a confusion matrix using confusionMatrix() of caret.
gwr.fixed$y <- as.factor(gwr.fixed$y)
gwr.fixed$most <- as.factor(gwr.fixed$most)
CM <- confusionMatrix(data=gwr.fixed$most,
reference=gwr.fixed$y,
positive="TRUE")
CMConfusion Matrix and Statistics
Reference
Prediction FALSE TRUE
FALSE 1824 263
TRUE 290 2379
Accuracy : 0.8837
95% CI : (0.8743, 0.8927)
No Information Rate : 0.5555
P-Value [Acc > NIR] : <2e-16
Kappa : 0.7642
Mcnemar's Test P-Value : 0.2689
Sensitivity : 0.9005
Specificity : 0.8628
Pos Pred Value : 0.8913
Neg Pred Value : 0.8740
Prevalence : 0.5555
Detection Rate : 0.5002
Detection Prevalence : 0.5612
Balanced Accuracy : 0.8816
'Positive' Class : TRUE
Things to note:
Accuracy, Sensitivity and Specificity scores of the GWLR model has improved as compared to the Global LR model
Model Accuracy Sensitivity Specificity Global LR 0.6739 0.7207 0.6154 GLWR Model 0.8837 0.9005 0.8628 Based on the above comparison, including spatial attributes will improve the explanatory power of the model. The results also show that the strategies to manage and maintain water points should be localised by taking into consideration the neighboring LGAs.
7.9.5 Visualise the results of the GWLR model
We will first extract the administrative boundary details into a new data frame.
Osun_wp_sf_selected <- Osun_wp_sf_clean %>%
select(c(ADM2_EN, ADM2_PCODE,ADM1_EN,ADM1_PCODE,status))Next, we will combine the new data frame with the model results
gwr_sf.fixed <- cbind(Osun_wp_sf_selected, gwr.fixed)Now we will plot the actual status of functional and non-functional water points (left map) and place the status generated by the gwlr model next to it (right map) for ease of comparison.
tmap_mode("view")tmap mode set to interactive viewingprob_T <- tm_shape(Osun) +
tm_polygons(alpha = 0.1) +
tm_shape(gwr_sf.fixed) +
tm_dots(col = "most",
border.col = "gray60",
border.lwd = 1) +
tm_layout(main.title = "Predicted Status of Water Points",
main.title.position = "center",
main.title.size = 1.0) +
tm_view(set.zoom.limits = c(9,12))
tmap_arrange(actual_status, prob_T,
asp=1, ncol=2, nrow = 1,
sync = TRUE)We can observe that the location of functional (TRUE) and non-functional (FALSE) water points on both plots are almost identical (justifying the 88% accuracy 😜) .
7.10 Revised Global LR and GWLR models by removing the statistically non-significant dependent variables.
In Section 7.8 above, we discovered that distance_to_primary_road and distance_to_secondary_road are not statistically significant variables and can be excluded from the model. We will now update the Global LR and GWLR models by excluding the 2 variables. We will be largely repeating the steps covered in Sections 7.8 and 7.9.
7.10.1 Build a Global Logistic Regression Model without non-significant dependent variables
We fit the model in step 1 and then generate the model results in step 2
# Step 1:
revised_model <- glm(status ~ distance_to_tertiary_road +
distance_to_city +
distance_to_town +
is_urban +
usage_capacity +
water_source_clean +
water_point_population +
local_population_1km,
data = Osun_wp_sf_clean,
family = binomial(link = "logit"))
# Step 2"
blr_regress(revised_model) Model Overview
------------------------------------------------------------------------
Data Set Resp Var Obs. Df. Model Df. Residual Convergence
------------------------------------------------------------------------
data status 4756 4755 4746 TRUE
------------------------------------------------------------------------
Response Summary
--------------------------------------------------------
Outcome Frequency Outcome Frequency
--------------------------------------------------------
0 2114 1 2642
--------------------------------------------------------
Maximum Likelihood Estimates
-----------------------------------------------------------------------------------------------
Parameter DF Estimate Std. Error z value Pr(>|z|)
-----------------------------------------------------------------------------------------------
(Intercept) 1 0.3540 0.1055 3.3541 8e-04
distance_to_tertiary_road 1 1e-04 0.0000 4.9096 0.0000
distance_to_city 1 0.0000 0.0000 -5.2022 0.0000
distance_to_town 1 0.0000 0.0000 -5.4660 0.0000
is_urbanTRUE 1 -0.2667 0.0747 -3.5690 4e-04
usage_capacity1000 1 -0.6206 0.0697 -8.9081 0.0000
water_source_cleanProtected Shallow Well 1 0.4947 0.0850 5.8228 0.0000
water_source_cleanProtected Spring 1 1.2790 0.4384 2.9174 0.0035
water_point_population 1 -5e-04 0.0000 -11.3902 0.0000
local_population_1km 1 3e-04 0.0000 19.4069 0.0000
-----------------------------------------------------------------------------------------------
Association of Predicted Probabilities and Observed Responses
---------------------------------------------------------------
% Concordant 0.7349 Somers' D 0.4697
% Discordant 0.2651 Gamma 0.4697
% Tied 0.0000 Tau-a 0.2320
Pairs 5585188 c 0.7349
---------------------------------------------------------------- We observe that the p-value of the remaining dependent variables are all < 0.05, indicating that they are statisitically significant.
Next, we evaluate the performance metrics of the model using blr_confusion_matrix() of blorr.
blr_confusion_matrix(revised_model,cutoff = 0.5)Confusion Matrix and Statistics
Reference
Prediction FALSE TRUE
0 1300 743
1 814 1899
Accuracy : 0.6726
No Information Rate : 0.4445
Kappa : 0.3348
McNemars's Test P-Value : 0.0761
Sensitivity : 0.7188
Specificity : 0.6149
Pos Pred Value : 0.7000
Neg Pred Value : 0.6363
Prevalence : 0.5555
Detection Rate : 0.3993
Detection Prevalence : 0.5704
Balanced Accuracy : 0.6669
Precision : 0.7000
Recall : 0.7188
'Positive' Class : 1- We note there’s no substantial change in the Accuracy, Sensitivity and Specificity scores from the previous Global Logistic Regression model
7.10.2 Derive the revised Fixed Bandwidth for the GWLR Model
revised_bw.fixed <- bw.ggwr(status ~ distance_to_tertiary_road +
distance_to_city +
distance_to_town +
water_point_population +
local_population_1km +
usage_capacity +
is_urban +
water_source_clean,
data = Osun_wp_sp,
family = "binomial",
approach = "AIC",
kernel = "gaussian",
adaptive = FALSE,
longlat = FALSE)Take a cup of tea and have a break, it will take a few minutes.
-----A kind suggestion from GWmodel development group
Iteration Log-Likelihood:(With bandwidth: 95768.67 )
=========================
0 -2890
1 -2837
2 -2830
3 -2829
4 -2829
5 -2829
Fixed bandwidth: 95768.67 AICc value: 5681.18
Iteration Log-Likelihood:(With bandwidth: 59200.13 )
=========================
0 -2878
1 -2820
2 -2812
3 -2810
4 -2810
5 -2810
Fixed bandwidth: 59200.13 AICc value: 5645.901
Iteration Log-Likelihood:(With bandwidth: 36599.53 )
=========================
0 -2854
1 -2790
2 -2777
3 -2774
4 -2774
5 -2774
6 -2774
Fixed bandwidth: 36599.53 AICc value: 5585.354
Iteration Log-Likelihood:(With bandwidth: 22631.59 )
=========================
0 -2810
1 -2732
2 -2711
3 -2707
4 -2707
5 -2707
6 -2707
Fixed bandwidth: 22631.59 AICc value: 5481.877
Iteration Log-Likelihood:(With bandwidth: 13998.93 )
=========================
0 -2732
1 -2635
2 -2604
3 -2597
4 -2596
5 -2596
6 -2596
Fixed bandwidth: 13998.93 AICc value: 5333.718
Iteration Log-Likelihood:(With bandwidth: 8663.649 )
=========================
0 -2624
1 -2502
2 -2459
3 -2447
4 -2446
5 -2446
6 -2446
7 -2446
Fixed bandwidth: 8663.649 AICc value: 5178.493
Iteration Log-Likelihood:(With bandwidth: 5366.266 )
=========================
0 -2478
1 -2319
2 -2250
3 -2225
4 -2219
5 -2219
6 -2220
7 -2220
8 -2220
9 -2220
Fixed bandwidth: 5366.266 AICc value: 5022.016
Iteration Log-Likelihood:(With bandwidth: 3328.371 )
=========================
0 -2222
1 -2002
2 -1894
3 -1838
4 -1818
5 -1814
6 -1814
Fixed bandwidth: 3328.371 AICc value: 4827.587
Iteration Log-Likelihood:(With bandwidth: 2068.882 )
=========================
0 -1837
1 -1528
2 -1357
3 -1261
4 -1222
5 -1222
Fixed bandwidth: 2068.882 AICc value: 4772.046
Iteration Log-Likelihood:(With bandwidth: 1290.476 )
=========================
0 -1403
1 -1016
2 -807.3
3 -680.2
4 -680.2
Fixed bandwidth: 1290.476 AICc value: 5809.721
Iteration Log-Likelihood:(With bandwidth: 2549.964 )
=========================
0 -2019
1 -1753
2 -1614
3 -1538
4 -1506
5 -1506
Fixed bandwidth: 2549.964 AICc value: 4764.056
Iteration Log-Likelihood:(With bandwidth: 2847.289 )
=========================
0 -2108
1 -1862
2 -1736
3 -1670
4 -1644
5 -1644
Fixed bandwidth: 2847.289 AICc value: 4791.834
Iteration Log-Likelihood:(With bandwidth: 2366.207 )
=========================
0 -1955
1 -1675
2 -1525
3 -1441
4 -1407
5 -1407
Fixed bandwidth: 2366.207 AICc value: 4755.524
Iteration Log-Likelihood:(With bandwidth: 2252.639 )
=========================
0 -1913
1 -1623
2 -1465
3 -1376
4 -1341
5 -1341
Fixed bandwidth: 2252.639 AICc value: 4759.188
Iteration Log-Likelihood:(With bandwidth: 2436.396 )
=========================
0 -1980
1 -1706
2 -1560
3 -1479
4 -1446
5 -1446
Fixed bandwidth: 2436.396 AICc value: 4756.675
Iteration Log-Likelihood:(With bandwidth: 2322.828 )
=========================
0 -1940
1 -1656
2 -1503
3 -1417
4 -1382
5 -1382
Fixed bandwidth: 2322.828 AICc value: 4756.471
Iteration Log-Likelihood:(With bandwidth: 2393.017 )
=========================
0 -1965
1 -1687
2 -1539
3 -1456
4 -1422
5 -1422
Fixed bandwidth: 2393.017 AICc value: 4755.57
Iteration Log-Likelihood:(With bandwidth: 2349.638 )
=========================
0 -1949
1 -1668
2 -1517
3 -1432
4 -1398
5 -1398
Fixed bandwidth: 2349.638 AICc value: 4755.753
Iteration Log-Likelihood:(With bandwidth: 2376.448 )
=========================
0 -1959
1 -1680
2 -1530
3 -1447
4 -1413
5 -1413
Fixed bandwidth: 2376.448 AICc value: 4755.48
Iteration Log-Likelihood:(With bandwidth: 2382.777 )
=========================
0 -1961
1 -1683
2 -1534
3 -1450
4 -1416
5 -1416
Fixed bandwidth: 2382.777 AICc value: 4755.491
Iteration Log-Likelihood:(With bandwidth: 2372.536 )
=========================
0 -1958
1 -1678
2 -1528
3 -1445
4 -1411
5 -1411
Fixed bandwidth: 2372.536 AICc value: 4755.488
Iteration Log-Likelihood:(With bandwidth: 2378.865 )
=========================
0 -1960
1 -1681
2 -1532
3 -1448
4 -1414
5 -1414
Fixed bandwidth: 2378.865 AICc value: 4755.481
Iteration Log-Likelihood:(With bandwidth: 2374.954 )
=========================
0 -1959
1 -1679
2 -1530
3 -1446
4 -1412
5 -1412
Fixed bandwidth: 2374.954 AICc value: 4755.482
Iteration Log-Likelihood:(With bandwidth: 2377.371 )
=========================
0 -1959
1 -1680
2 -1531
3 -1447
4 -1413
5 -1413
Fixed bandwidth: 2377.371 AICc value: 4755.48
Iteration Log-Likelihood:(With bandwidth: 2377.942 )
=========================
0 -1960
1 -1680
2 -1531
3 -1448
4 -1414
5 -1414
Fixed bandwidth: 2377.942 AICc value: 4755.48
Iteration Log-Likelihood:(With bandwidth: 2377.018 )
=========================
0 -1959
1 -1680
2 -1531
3 -1447
4 -1413
5 -1413
Fixed bandwidth: 2377.018 AICc value: 4755.48 revised_bw.fixed[1] 2377.371The derived bandwidth is 2377.371 metres.
7.10.3 Fit the revised Fixed Bandwidth and data to the GWLR model
We fit a revised model using the updated bandwidth obtained above.
revised_gwlr.fixed <- ggwr.basic(status ~ distance_to_tertiary_road +
distance_to_city +
distance_to_town +
water_point_population +
local_population_1km +
usage_capacity +
is_urban +
water_source_clean,
data = Osun_wp_sp,
bw=2377.371,
family = "binomial",
kernel = "gaussian",
adaptive = FALSE,
longlat = FALSE)Warning in proj4string(data): CRS object has comment, which is lost in output; in tests, see
https://cran.r-project.org/web/packages/sp/vignettes/CRS_warnings.htmlWarning in proj4string(regression.points): CRS object has comment, which is lost in output; in tests, see
https://cran.r-project.org/web/packages/sp/vignettes/CRS_warnings.html Iteration Log-Likelihood
=========================
0 -1959
1 -1680
2 -1531
3 -1447
4 -1413
5 -1413 We review the results of the revised model.
revised_gwlr.fixed ***********************************************************************
* Package GWmodel *
***********************************************************************
Program starts at: 2022-12-18 00:12:30
Call:
ggwr.basic(formula = status ~ distance_to_tertiary_road + distance_to_city +
distance_to_town + water_point_population + local_population_1km +
usage_capacity + is_urban + water_source_clean, data = Osun_wp_sp,
bw = 2377.371, family = "binomial", kernel = "gaussian",
adaptive = FALSE, longlat = FALSE)
Dependent (y) variable: status
Independent variables: distance_to_tertiary_road distance_to_city distance_to_town water_point_population local_population_1km usage_capacity is_urban water_source_clean
Number of data points: 4756
Used family: binomial
***********************************************************************
* Results of Generalized linear Regression *
***********************************************************************
Call:
NULL
Deviance Residuals:
Min 1Q Median 3Q Max
-129.368 -1.750 1.074 1.742 34.126
Coefficients:
Estimate Std. Error z value Pr(>|z|)
Intercept 3.540e-01 1.055e-01 3.354 0.000796
distance_to_tertiary_road 1.001e-04 2.040e-05 4.910 9.13e-07
distance_to_city -1.764e-05 3.391e-06 -5.202 1.97e-07
distance_to_town -1.544e-05 2.825e-06 -5.466 4.60e-08
water_point_population -5.098e-04 4.476e-05 -11.390 < 2e-16
local_population_1km 3.452e-04 1.779e-05 19.407 < 2e-16
usage_capacity1000 -6.206e-01 6.966e-02 -8.908 < 2e-16
is_urbanTRUE -2.667e-01 7.474e-02 -3.569 0.000358
water_source_cleanProtected Shallow Well 4.947e-01 8.496e-02 5.823 5.79e-09
water_source_cleanProtected Spring 1.279e+00 4.384e-01 2.917 0.003530
Intercept ***
distance_to_tertiary_road ***
distance_to_city ***
distance_to_town ***
water_point_population ***
local_population_1km ***
usage_capacity1000 ***
is_urbanTRUE ***
water_source_cleanProtected Shallow Well ***
water_source_cleanProtected Spring **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 6534.5 on 4755 degrees of freedom
Residual deviance: 5688.9 on 4746 degrees of freedom
AIC: 5708.9
Number of Fisher Scoring iterations: 5
AICc: 5708.923
Pseudo R-square value: 0.129406
***********************************************************************
* Results of Geographically Weighted Regression *
***********************************************************************
*********************Model calibration information*********************
Kernel function: gaussian
Fixed bandwidth: 2377.371
Regression points: the same locations as observations are used.
Distance metric: A distance matrix is specified for this model calibration.
************Summary of Generalized GWR coefficient estimates:**********
Min. 1st Qu. Median
Intercept -3.7021e+02 -4.3797e+00 3.5590e+00
distance_to_tertiary_road -3.1622e-02 -4.5462e-04 9.1291e-05
distance_to_city -5.4555e-02 -6.5623e-04 -1.3507e-04
distance_to_town -8.6549e-03 -5.2754e-04 -1.6785e-04
water_point_population -2.9696e-02 -2.2705e-03 -1.2277e-03
local_population_1km -7.7730e-02 4.4281e-04 1.0548e-03
usage_capacity1000 -5.5889e+01 -1.0347e+00 -4.1960e-01
is_urbanTRUE -7.3554e+02 -3.4675e+00 -1.6596e+00
water_source_cleanProtected.Shallow.Well -1.8842e+02 -4.7295e-01 6.2378e-01
water_source_cleanProtected.Spring -1.3630e+03 -5.3436e+00 2.7714e+00
3rd Qu. Max.
Intercept 1.3755e+01 2171.6375
distance_to_tertiary_road 6.3011e-04 0.0237
distance_to_city 1.5921e-04 0.0162
distance_to_town 2.4490e-04 0.0179
water_point_population 4.5879e-04 0.0765
local_population_1km 1.8479e-03 0.0333
usage_capacity1000 3.9113e-01 9.2449
is_urbanTRUE 1.0554e+00 995.1841
water_source_cleanProtected.Shallow.Well 1.9564e+00 66.8914
water_source_cleanProtected.Spring 7.0805e+00 208.3749
************************Diagnostic information*************************
Number of data points: 4756
GW Deviance: 2815.659
AIC : 4418.776
AICc : 4744.213
Pseudo R-square value: 0.5691072
***********************************************************************
Program stops at: 2022-12-18 00:12:58 A comparison of the AICc of the models with and without the non-significant dependent variables is as follows:
| Model | With non-significant dependent variables | Without non-significant dependent variables |
|---|---|---|
| Global LR | 5712.099 | 5708.923 |
| GLWR Model | 4747.423 | 4744.213 |
There is only a marginal change in the AICc results of the models after we remove the non-significant variables.
We go on to assess the model performance of the revised GWLR model by constructing the confusion matrix using the confusionMatrix() of caret.
# Step 1: Convert the SDF object of the gwlr model into a data frame
revised_gwr.fixed <- as.data.frame(revised_gwlr.fixed$SDF)
# Step 2: Include a new column most that indicate if the modelled results
revised_gwr.fixed <- revised_gwr.fixed %>%
mutate(most = ifelse(
revised_gwr.fixed$yhat >= 0.5,T,F))
# Step 3: Generate the performance metrics
revised_gwr.fixed$y <- as.factor(revised_gwr.fixed$y)
revised_gwr.fixed$most <- as.factor(revised_gwr.fixed$most)
CM <- confusionMatrix(data=revised_gwr.fixed$most,
reference=revised_gwr.fixed$y,
positive="TRUE")
CMConfusion Matrix and Statistics
Reference
Prediction FALSE TRUE
FALSE 1833 268
TRUE 281 2374
Accuracy : 0.8846
95% CI : (0.8751, 0.8935)
No Information Rate : 0.5555
P-Value [Acc > NIR] : <2e-16
Kappa : 0.7661
Mcnemar's Test P-Value : 0.6085
Sensitivity : 0.8986
Specificity : 0.8671
Pos Pred Value : 0.8942
Neg Pred Value : 0.8724
Prevalence : 0.5555
Detection Rate : 0.4992
Detection Prevalence : 0.5582
Balanced Accuracy : 0.8828
'Positive' Class : TRUE
We tabulate the performance metrics of the 4 models as follow
| Model | Accuracy | Sensitivity | Specificity |
|---|---|---|---|
Global LR (With non-significant dependent variables) |
0.6739 | 0.7207 | 0.6154 |
GLWR Model (With non-significant dependent variables) |
0.8837 | 0.9005 | 0.8628 |
Global LR (Without non-significant dependent variables) |
0.6726 | 0.7188 | 0.6149 |
GLWR Model (Without non-significant dependent variables) |
0.8846 | 0.8986 | 0.8671 |
As we can see from the above, the inclusion of statistically non-significant variables do not adversely affect the performance of logistic regression models (differences of <0.01), be it non-spatial or geographically weighted. For computational efficiency, we should exclude the dependent variables (i.e. noise) from the modelling process once they are determined to be non-significant. Also, from an explanatory modelling perspective, the results above provide evidence that the distance of water points to primary or secondary roads are not relevant to the functional status of the water points.
7.11 Conclusion
From the data that is used for modelling, it is evident from the generated AICc that Geographically Weighted models provide better explanatory power about the status of the water points as compared to a non-spatial (or Global) Logistic Regression models. The administrators of Osun State Nigeria could make use of the coefficient estimates derived for the 8 dependent variables of each water point to understand the factors that contribute to its functional status and device measures to prevent the water point from malfunctioning.
References
- Wikipedia write-up on Osun State of Nigeria, Osun State - Wikipedia