pacman::p_load(rgdal, spdep, tmap, sf,
ggpubr, cluster, factoextra, NbClust, GGally,
heatmaply, corrplot, psych, tidyverse, ClustGeo)Hands-On Exercise 3/ In-Class Exercise 3
Updated on: 13-Dec-2022
(First published on: 2-Dec-2022)
5 Geographical Segmentation with Spatially Constrained Clustering Techniques
5.1 Overview
In this hands-on exercise, we will learn how to delineate homogeneous regions by using geographically referenced multivariate data.
There are two major analysis, namely:
hierarchical cluster analysis; and
spatially constrained cluster analysis.
5.1.1 Learning outcomes
By the end of this hands-on exercise, we will be able to:
convert GIS polygon data into R’s simple feature (sf) data.frame by using appropriate functions of sf package;
convert sf data.frame into R’s SpatialPolygonDataFrame object by using appropriate sf of package;
perform custer analysis by using
hclust()of Base R;perform spatially constrained cluster analysis using
skater()of Base R; andto visualise the analysis outputs by using ggplot2 and tmap package
5.2 Getting started
5.2.1 The analytical question
In this hands-on exercise, we are interested to delineate Shan State, Myanmar into homogeneous regions by using multiple Information and Communication technology (ICT) measures, namely: Radio, Television, Land line phone, Mobile phone, Computer, and Internet at home.
5.3 The data
The 2 data sets used in this exercise are:
Myanmar Township Boundary Data (i.e. myanmar_township_boundaries) : This is a GIS data in ESRI shapefile format. It consists of township boundary information of Myanmar. The spatial data are captured in polygon features.
Shan-ICT.csv: This is an extract of The 2014 Myanmar Population and Housing Census Myanmar at the township level.
Both data sets are download from Myanmar Information Management Unit (MIMU)
5.3.1 Installing and loading R packages
Before we get started, it is important for us to install the necessary R packages into R and launch these R packages into R environment.
The R packages needed for this exercise are as follows:
Spatial data handling - sf, rgdal and spdep
Attribute data handling - tidyverse, especially readr, ggplot2 and dplyr
Choropleth mapping - tmap
Multivariate data visualisation and analysis - corrplot, ggpubr, GGally and heatmaply
Cluster analysis - cluster, and ClustGeo
The code chunk below installs and launches these R packages into R environment.
5.4 Data Import and Prepatation
5.4.1 Importing geospatial data into R environment
The Myanmar Township Boundary GIS data is in ESRI shapefile format. It will be imported into R environment by using the st_read() function of sf.
The code chunk used is shown below:
shan_sf <- st_read(dsn = "Hands-On_Ex3/data/geospatial",
layer = "myanmar_township_boundaries") %>%
filter(ST %in% c("Shan (East)", "Shan (North)", "Shan (South)")) %>%
select(c(2:7))Reading layer `myanmar_township_boundaries' from data source
`C:\Cabbie-UK\ISSS624\Hands-On_Ex\Hands-On_Ex3\data\geospatial'
using driver `ESRI Shapefile'
Simple feature collection with 330 features and 14 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 92.17275 ymin: 9.671252 xmax: 101.1699 ymax: 28.54554
Geodetic CRS: WGS 84The imported township boundary object is called shan_sf. It is saved in simple feature data.frame format. We can view the content of the newly created shan_sf simple features data.frame by using the code chunk below.
shan_sfSimple feature collection with 55 features and 6 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 96.15107 ymin: 19.29932 xmax: 101.1699 ymax: 24.15907
Geodetic CRS: WGS 84
First 10 features:
ST ST_PCODE DT DT_PCODE TS TS_PCODE
1 Shan (North) MMR015 Mongmit MMR015D008 Mongmit MMR015017
2 Shan (South) MMR014 Taunggyi MMR014D001 Pindaya MMR014006
3 Shan (South) MMR014 Taunggyi MMR014D001 Ywangan MMR014007
4 Shan (South) MMR014 Taunggyi MMR014D001 Pinlaung MMR014009
5 Shan (North) MMR015 Mongmit MMR015D008 Mabein MMR015018
6 Shan (South) MMR014 Taunggyi MMR014D001 Kalaw MMR014005
7 Shan (South) MMR014 Taunggyi MMR014D001 Pekon MMR014010
8 Shan (South) MMR014 Taunggyi MMR014D001 Lawksawk MMR014008
9 Shan (North) MMR015 Kyaukme MMR015D003 Nawnghkio MMR015013
10 Shan (North) MMR015 Kyaukme MMR015D003 Kyaukme MMR015012
geometry
1 MULTIPOLYGON (((96.96001 23...
2 MULTIPOLYGON (((96.7731 21....
3 MULTIPOLYGON (((96.78483 21...
4 MULTIPOLYGON (((96.49518 20...
5 MULTIPOLYGON (((96.66306 24...
6 MULTIPOLYGON (((96.49518 20...
7 MULTIPOLYGON (((97.14738 19...
8 MULTIPOLYGON (((96.94981 22...
9 MULTIPOLYGON (((96.75648 22...
10 MULTIPOLYGON (((96.95498 22...Notice that sf.data.frame conforms to Hardy Wickham’s tidy framework. Since shan_sf is conformed to tidy framework, we can also glimpse() to reveal the data type of it’s fields.
glimpse(shan_sf)Rows: 55
Columns: 7
$ ST <chr> "Shan (North)", "Shan (South)", "Shan (South)", "Shan (South)…
$ ST_PCODE <chr> "MMR015", "MMR014", "MMR014", "MMR014", "MMR015", "MMR014", "…
$ DT <chr> "Mongmit", "Taunggyi", "Taunggyi", "Taunggyi", "Mongmit", "Ta…
$ DT_PCODE <chr> "MMR015D008", "MMR014D001", "MMR014D001", "MMR014D001", "MMR0…
$ TS <chr> "Mongmit", "Pindaya", "Ywangan", "Pinlaung", "Mabein", "Kalaw…
$ TS_PCODE <chr> "MMR015017", "MMR014006", "MMR014007", "MMR014009", "MMR01501…
$ geometry <MULTIPOLYGON [°]> MULTIPOLYGON (((96.96001 23..., MULTIPOLYGON (((…5.4.2 Importing aspatial data into R environment
The csv file will be import using read_csv() of readr package.
The code chunk used is shown below:
ict <- read_csv ("Hands-On_Ex3/data/aspatial/Shan-ICT.csv", show_col_types = FALSE)The attribute data set is called ict. It is saved in R’s * tibble data.frame* format.
The code chunk below reveals the summary statistics of ict data.frame.
summary(ict) District Pcode District Name Township Pcode Township Name
Length:55 Length:55 Length:55 Length:55
Class :character Class :character Class :character Class :character
Mode :character Mode :character Mode :character Mode :character
Total households Radio Television Land line phone
Min. : 3318 Min. : 115 Min. : 728 Min. : 20.0
1st Qu.: 8711 1st Qu.: 1260 1st Qu.: 3744 1st Qu.: 266.5
Median :13685 Median : 2497 Median : 6117 Median : 695.0
Mean :18369 Mean : 4487 Mean :10183 Mean : 929.9
3rd Qu.:23471 3rd Qu.: 6192 3rd Qu.:13906 3rd Qu.:1082.5
Max. :82604 Max. :30176 Max. :62388 Max. :6736.0
Mobile phone Computer Internet at home
Min. : 150 Min. : 20.0 Min. : 8.0
1st Qu.: 2037 1st Qu.: 121.0 1st Qu.: 88.0
Median : 3559 Median : 244.0 Median : 316.0
Mean : 6470 Mean : 575.5 Mean : 760.2
3rd Qu.: 7177 3rd Qu.: 507.0 3rd Qu.: 630.5
Max. :48461 Max. :6705.0 Max. :9746.0 5.4.3 Derive new variables using dplyr package
The unit of measurement of the values is the number of households. Using such a measure directly will bias townships with smaller number of households which also means there are fewer households owning radio, TV, etc.
In order to overcome this problem, we will derive the penetration rate of each ICT variable by using the code chunk below.
ict_derived <- ict %>%
mutate(`RADIO_PR` = `Radio`/`Total households`*100) %>%
mutate(`TV_PR` = `Television`/`Total households`*100) %>%
mutate(`LLPHONE_PR` = `Land line phone`/`Total households`*100) %>%
mutate(`MPHONE_PR` = `Mobile phone`/`Total households`*100) %>%
mutate(`COMPUTER_PR` = `Computer`/`Total households`*100) %>%
mutate(`INTERNET_PR` = `Internet at home`/`Total households`*100) %>%
# rename some of the columns to match them to those used in the shapefile
rename(`DT_PCODE` =`District Pcode`,`DT`=`District Name`,
`TS_PCODE`=`Township Pcode`, `TS`=`Township Name`,
`TT_HOUSEHOLDS`=`Total households`,
`RADIO`=`Radio`, `TV`=`Television`,
`LLPHONE`=`Land line phone`, `MPHONE`=`Mobile phone`,
`COMPUTER`=`Computer`, `INTERNET`=`Internet at home`) 6 new fields have been added into the data.frame. They are RADIO_PR, TV_PR, LLPHONE_PR, MPHONE_PR, COMPUTER_PR, and INTERNET_PR.
Let us review the summary statistics of the newly derived penetration rates using the code chunk below.
summary(ict_derived) DT_PCODE DT TS_PCODE TS
Length:55 Length:55 Length:55 Length:55
Class :character Class :character Class :character Class :character
Mode :character Mode :character Mode :character Mode :character
TT_HOUSEHOLDS RADIO TV LLPHONE
Min. : 3318 Min. : 115 Min. : 728 Min. : 20.0
1st Qu.: 8711 1st Qu.: 1260 1st Qu.: 3744 1st Qu.: 266.5
Median :13685 Median : 2497 Median : 6117 Median : 695.0
Mean :18369 Mean : 4487 Mean :10183 Mean : 929.9
3rd Qu.:23471 3rd Qu.: 6192 3rd Qu.:13906 3rd Qu.:1082.5
Max. :82604 Max. :30176 Max. :62388 Max. :6736.0
MPHONE COMPUTER INTERNET RADIO_PR
Min. : 150 Min. : 20.0 Min. : 8.0 Min. : 2.105
1st Qu.: 2037 1st Qu.: 121.0 1st Qu.: 88.0 1st Qu.:13.895
Median : 3559 Median : 244.0 Median : 316.0 Median :21.095
Mean : 6470 Mean : 575.5 Mean : 760.2 Mean :21.568
3rd Qu.: 7177 3rd Qu.: 507.0 3rd Qu.: 630.5 3rd Qu.:26.807
Max. :48461 Max. :6705.0 Max. :9746.0 Max. :48.452
TV_PR LLPHONE_PR MPHONE_PR COMPUTER_PR
Min. :11.60 Min. : 0.278 Min. : 3.642 Min. :0.3278
1st Qu.:45.02 1st Qu.: 2.284 1st Qu.:19.014 1st Qu.:1.1832
Median :51.72 Median : 3.759 Median :30.527 Median :1.8970
Mean :50.95 Mean : 5.109 Mean :31.405 Mean :2.4393
3rd Qu.:60.64 3rd Qu.: 6.972 3rd Qu.:42.843 3rd Qu.:2.9897
Max. :84.25 Max. :18.149 Max. :73.543 Max. :9.2402
INTERNET_PR
Min. : 0.1041
1st Qu.: 0.8617
Median : 2.2829
Mean : 3.0644
3rd Qu.: 4.1281
Max. :11.7985 5.5 Exploratory Data Analysis (EDA)
5.5.1 EDA using statistical graphics
We can plot the distribution of the variables (i.e. Number of households with radio) by using appropriate Exploratory Data Analysis (EDA) as shown in the code chunk below.
Histogram is useful to identify the overall distribution of the data values (i.e. left skew, right skew or normal distribution)
ggplot(data=ict_derived,
aes(x=`RADIO`)) +
geom_histogram(bins=20,
color="black",
fill="light blue") +
ggtitle("Distribution of Households with radio")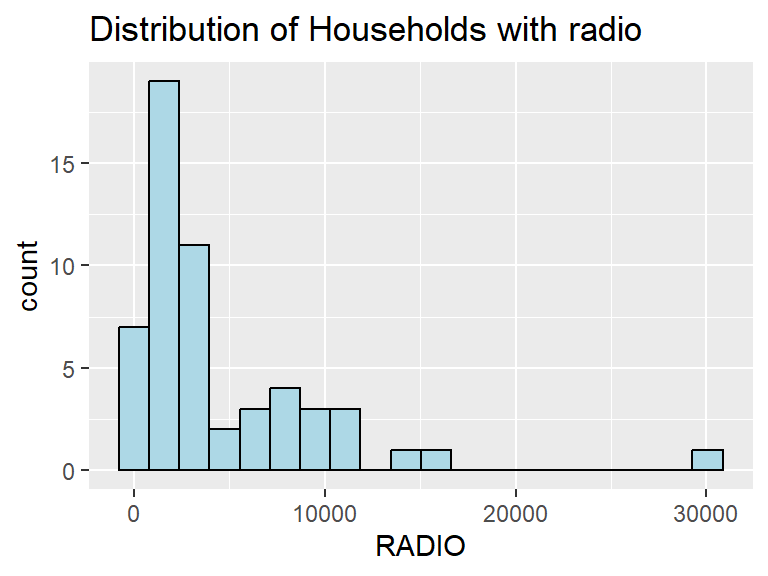
Boxplot is useful to detect if there are outliers in the data.
ggplot(data=ict_derived,
aes(x=`RADIO`)) +
geom_boxplot(color="black",
fill="light blue") +
ggtitle("Distribution of Househodls with radio (Boxplot)")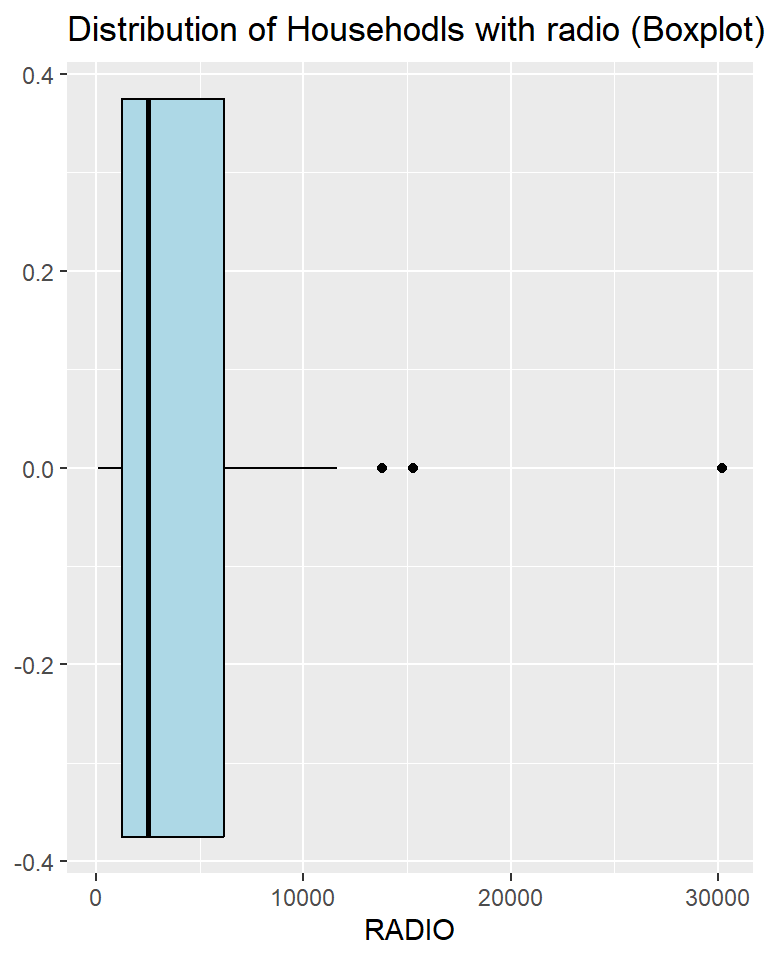
Next, we also plot the distribution of the newly derived variables (i.e. Radio penetration rate) by using the code chunk below.
ggplot(data=ict_derived,
aes(x=`RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue") +
ggtitle("Distribution of Radio Penetration Rate")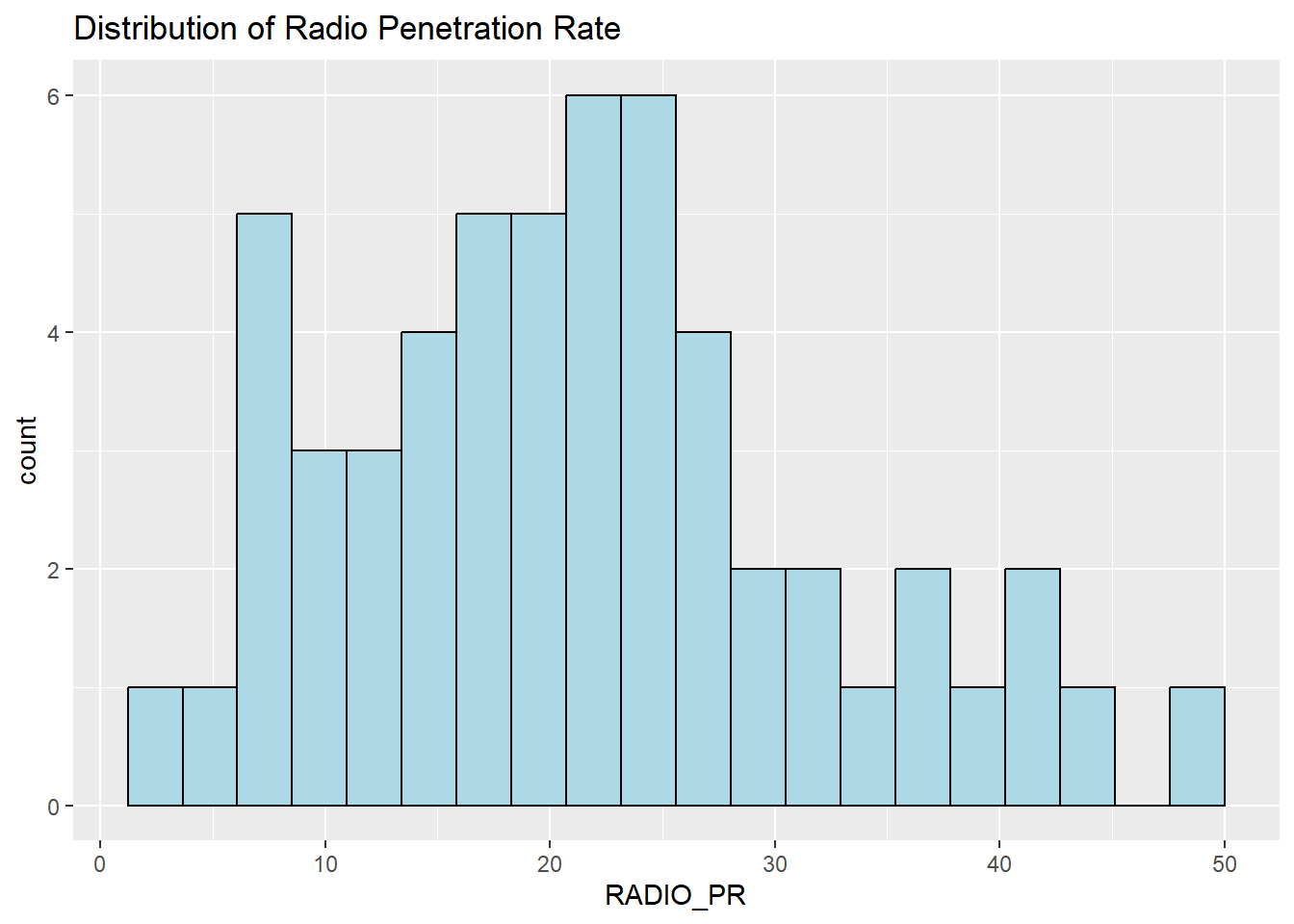
ggplot(data=ict_derived,
aes(x=`RADIO_PR`)) +
geom_boxplot(color="black",
fill="light blue") +
ggtitle("Distribution of Radio Penetration Rate \n(Boxplot)")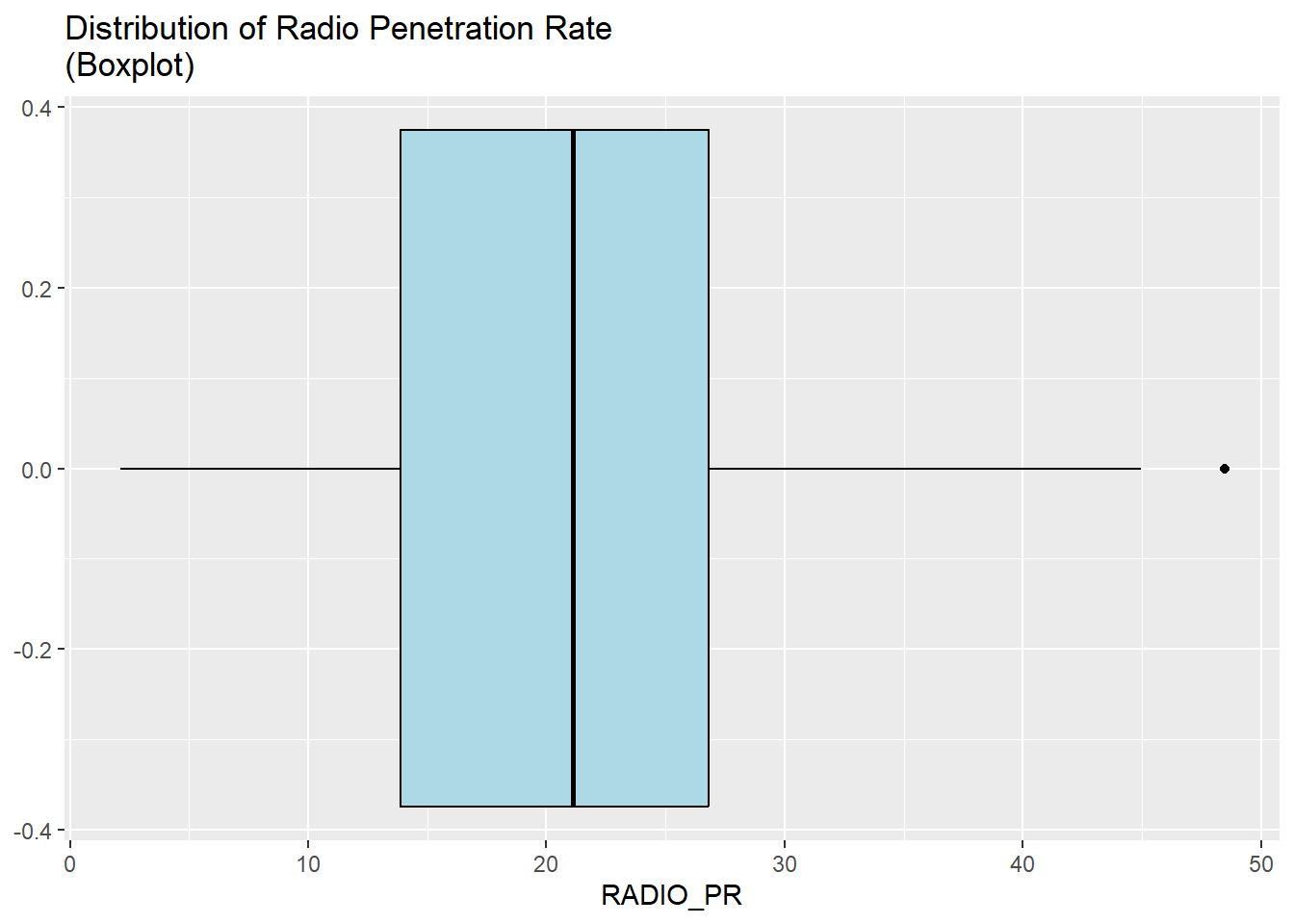
What can you observe from the distributions reveal in the histogram and boxplot? Reply: The distribution of the Radio Penetration Rate appears less skewed than the distribution of households with radio. From the boxplot, the number of outliers has reduced from 3 to 1. |
In the next code chunk below, multiple histograms are plotted to reveal the distribution of the selected variables in the ict_derived data.frame.
Step 1: We create the individual histograms using the code chunk below.
Step 2: We use the the
ggarange()function of ggpubr package to group these histograms together
# Step 1
radio <- ggplot(data=ict_derived,
aes(x= `RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
tv <- ggplot(data=ict_derived,
aes(x= `TV_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
llphone <- ggplot(data=ict_derived,
aes(x= `LLPHONE_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
mphone <- ggplot(data=ict_derived,
aes(x= `MPHONE_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
computer <- ggplot(data=ict_derived,
aes(x= `COMPUTER_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
internet <- ggplot(data=ict_derived,
aes(x= `INTERNET_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue")
# Step 2
ggarrange(radio, tv, llphone, mphone, computer, internet,
ncol = 3,
nrow = 2)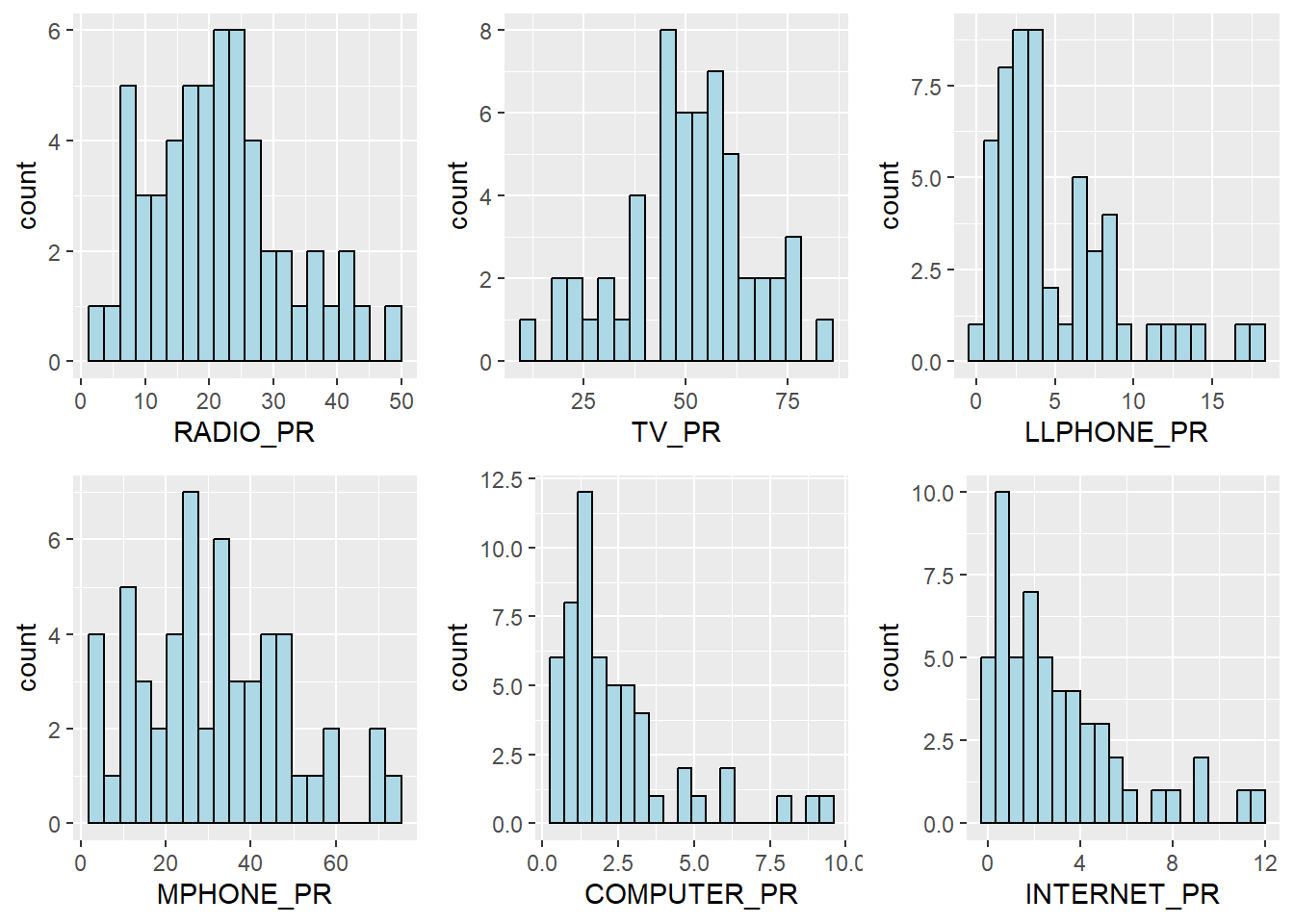
5.5.2 EDA using choropleth map
5.5.2.1 Joining geospatial data with aspatial data
Before we prepare the choropleth map, we need to combine both the geospatial data object (i.e. shan_sf) and aspatial data.frame object (i.e. ict_derived) into one. This will be performed by using the left_join function of dplyr package. The shan_sf simple feature data.frame will be used as the base data object and the ict_derived data.frame will be used as the join table.
The code chunks below is used to perform the task. The unique identifier used to join both data objects is TS_PCODE.
# if we want to retain the spatial data, the geospatial data file should be the left file. In this case, it's the shan_sf sf file.
shan_sf_joined <- left_join(shan_sf,
ict_derived, by=c("TS_PCODE"="TS_PCODE"))5.5.2.2 Preparing a choropleth map
For a quick look at the distribution of Radio penetration rate of Shan State at township level, a choropleth map is prepared.
The code chunk below is used to prepare the choroplethby using the qtm() function of tmap package.
qtm(shan_sf_joined, "RADIO_PR") +
tm_layout(main.title = "Radio Penetration Rate",
main.title.position = "center",
main.title.size = 1.2,
legend.height = 0.30,
legend.width = 0.30)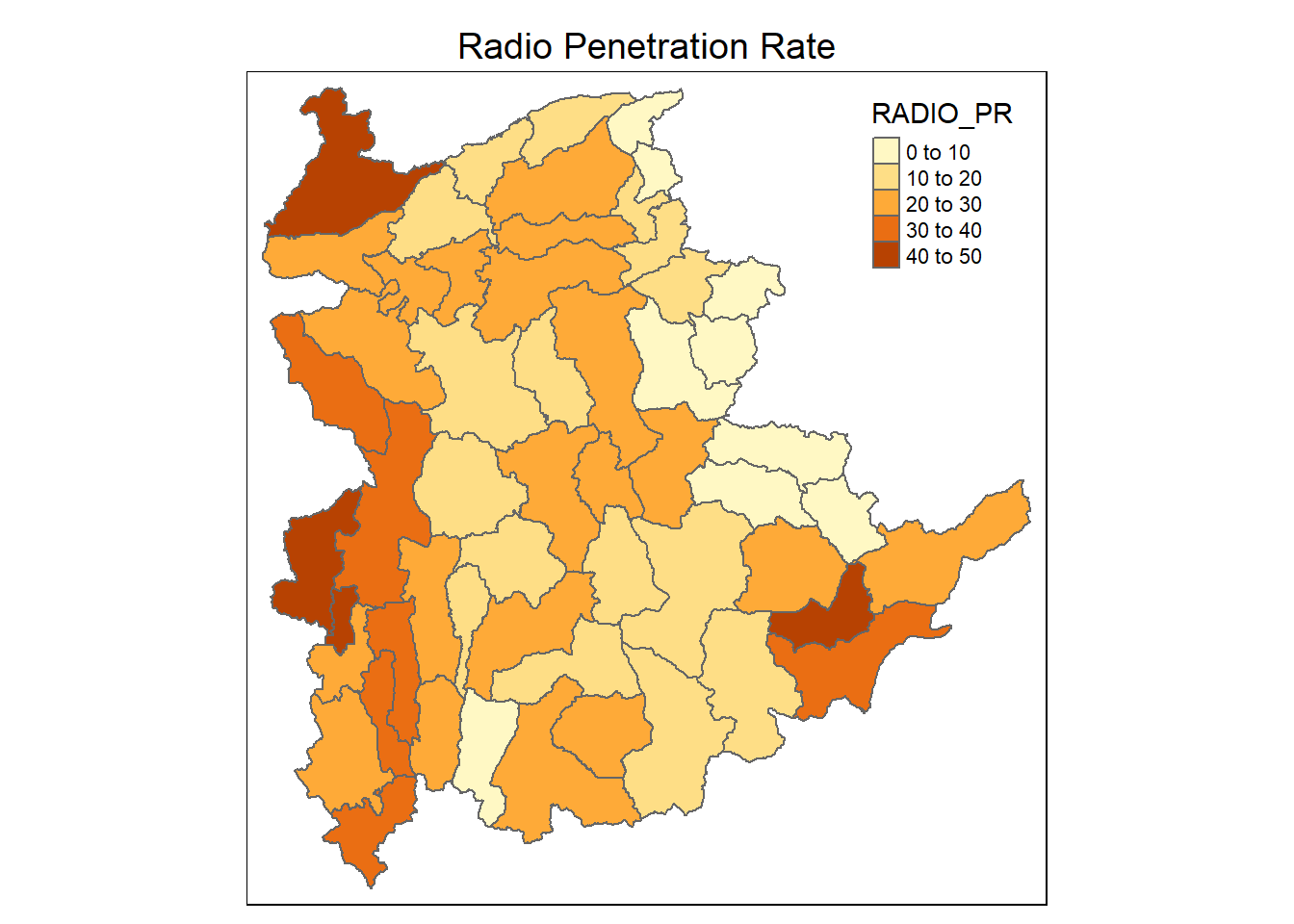
To demonstrate that the distribution shown in the choropleth map above are bias to the underlying total number of households at the townships, we create two choropleth maps, one for the total number of households (i.e. TT_HOUSEHOLDS.map) and one for the total number of household with Radio (RADIO.map) by using the code chunk below.
TT_HOUSEHOLDS.map <- tm_shape(shan_sf_joined) +
tm_fill(col = "TT_HOUSEHOLDS",
n = 5,
style = "jenks",
title = "Total households") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "Total number of households",
main.title.position = "center",
main.title.size = 1.2,
legend.height = 0.30,
legend.width = 0.30)
RADIO.map <- tm_shape(shan_sf_joined) +
tm_fill(col = "RADIO",
n = 5,
style = "jenks",
title = "Households with radio") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "Number of households with radio",
main.title.position = "center",
main.title.size = 1.2,
legend.height = 0.30,
legend.width = 0.30)
tmap_arrange(TT_HOUSEHOLDS.map, RADIO.map,
asp=NA, ncol=2)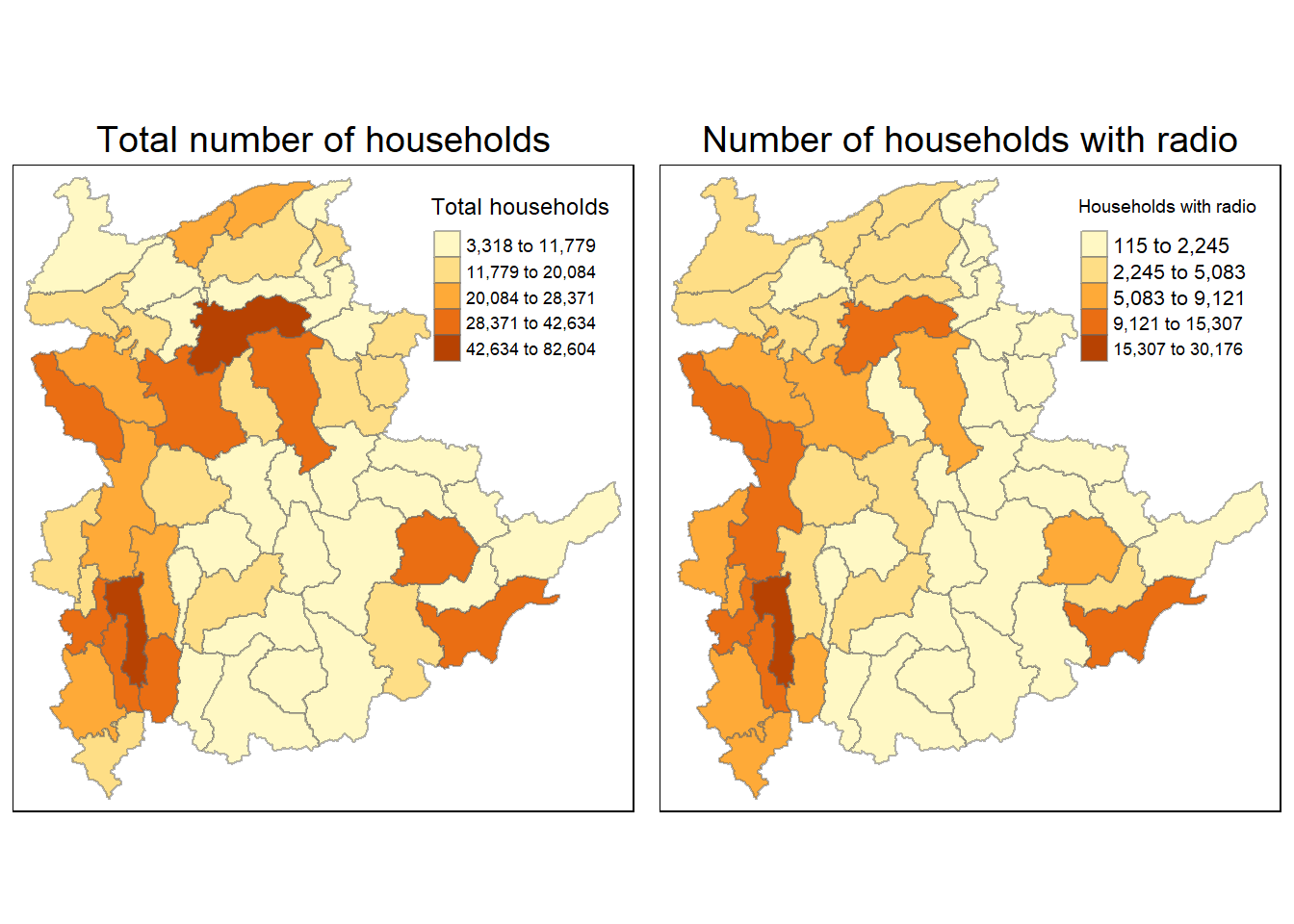
Notice that the choropleth maps above clearly show that townships with relatively larger number of households are also showing relatively higher number of radio ownership.
Now let us plot the choropleth maps showing the distribution of Number of households with radios and Radio penetration rate by using the code chunk below.
tm_shape(shan_sf_joined) +
tm_polygons(c("RADIO", "RADIO_PR"),
style="jenks") +
tm_facets(sync = TRUE, ncol = 2) +
tm_legend(legend.position = c("right", "bottom"))+
tm_layout(title = c("Number of households with radio","Radio Penetration Rate"),
outer.margins=0, asp=0)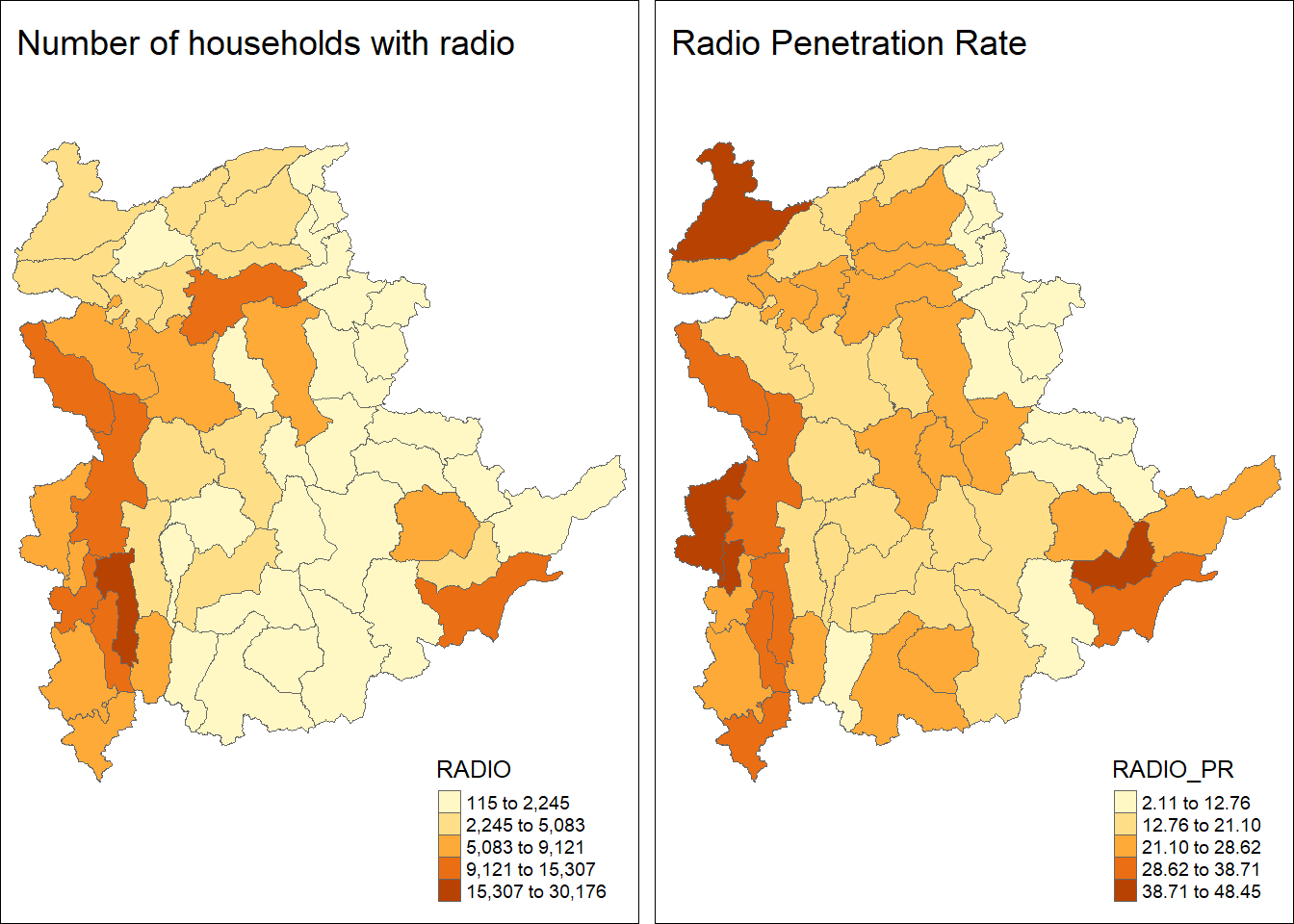
Can you identify the differences? From the 2 plots above, it is evident that regions with highest number of households in radios (on the left map) does not necessarily have the highest radio ownership rate (based on the right map) |
5.6 Correlation Analysis
Before we perform cluster analysis, it is important for us to ensure that the cluster variables are not highly correlated.
In this section, we use corrplot.mixed() function of corrplot package to visualise and analyse the correlation of the input variables.
# Only select columns 12 to 16 from the data.frame
cluster_vars.cor = cor(ict_derived[,12:17])
corrplot.mixed(cluster_vars.cor,
lower = "ellipse",
upper = "number",
tl.pos = "lt",
diag = "l",
tl.col = "black")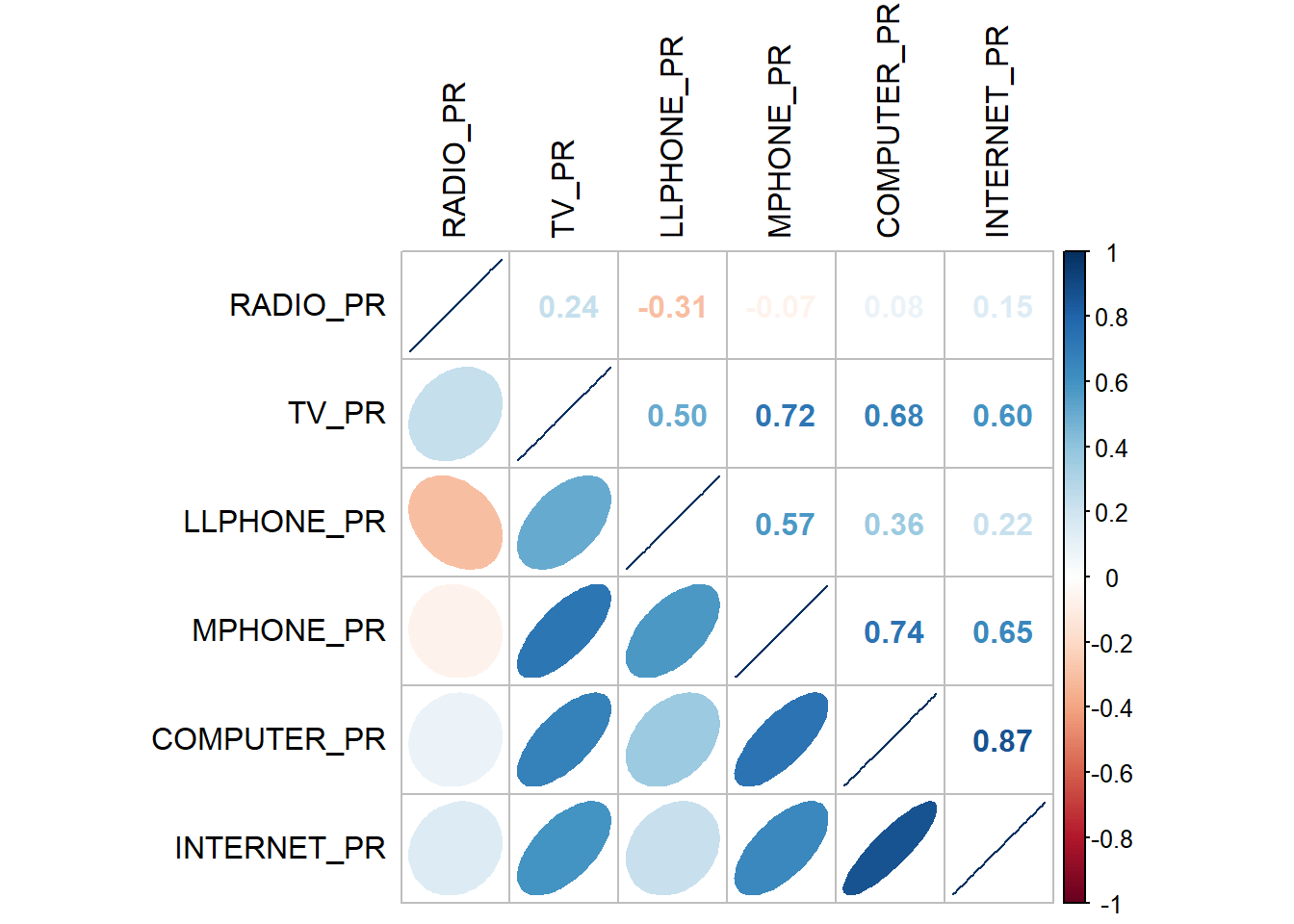
The correlation plot above shows that COMPUTER_PR and INTERNET_PR are highly correlated. This suggest that only one of them should be used in the cluster analysis instead of both.
5.7 Hierarchy Cluster Analysis
In this section, we learn how to perform hierarchical cluster analysis. The analysis consists of four major steps:
5.7.1 Extract clustering variables
The code chunk below extracts the clustering variables from the shan_sf_joined simple feature object into data.frame.
cluster_vars <- shan_sf_joined %>%
# The st_set_geometry is to remove the geomerty data from the final output
st_set_geometry(NULL) %>%
select("TS.x", "RADIO_PR", "TV_PR", "LLPHONE_PR", "MPHONE_PR", "COMPUTER_PR")
head(cluster_vars,10) TS.x RADIO_PR TV_PR LLPHONE_PR MPHONE_PR COMPUTER_PR
1 Mongmit 28.61852 55.41313 3.530618 26.06944 1.215939
2 Pindaya 41.74647 50.51300 1.983584 16.23917 1.288190
3 Ywangan 48.45215 26.05734 1.193591 12.02856 0.441465
4 Pinlaung 23.16499 54.17189 2.854454 24.94903 1.376255
5 Mabein 44.94903 70.86423 7.275255 39.26089 1.645042
6 Kalaw 28.07624 61.16204 4.206478 40.87951 2.963160
7 Pekon 31.86118 53.58494 3.983270 21.48476 1.897032
8 Lawksawk 38.71017 63.00035 3.151366 32.05686 2.176677
9 Nawnghkio 34.93359 54.79456 3.844960 32.30201 1.576465
10 Kyaukme 21.09548 60.11773 3.958267 37.24930 3.094709Notice that the final clustering variables list does not include variable INTERNET_PR because it is highly correlated with variable COMPUTER_PR.
Next, we set township name (Ts.x column) as the row names using the code chunk below so that the clustering algorithm won’t use the township name for clustering.
# Step 1: Assign the TS.x column as the row names of the cluster_var dataframe
row.names(cluster_vars) <- cluster_vars$"TS.x"
# Step 2:Exclude the TS.x coumn from the new shan_ict dataframe
shan_ict <- select(cluster_vars, c(2:6))
# Inspect the resultant dataframe
head(shan_ict) RADIO_PR TV_PR LLPHONE_PR MPHONE_PR COMPUTER_PR
Mongmit 28.61852 55.41313 3.530618 26.06944 1.215939
Pindaya 41.74647 50.51300 1.983584 16.23917 1.288190
Ywangan 48.45215 26.05734 1.193591 12.02856 0.441465
Pinlaung 23.16499 54.17189 2.854454 24.94903 1.376255
Mabein 44.94903 70.86423 7.275255 39.26089 1.645042
Kalaw 28.07624 61.16204 4.206478 40.87951 2.9631605.7.2 Data Standardisation
In general, multiple variables will be used in cluster analysis. It is not unusual their values range are different. In order to avoid the cluster analysis result that leans towards clustering variables with large values, it is useful to standardise the input variables before performing cluster analysis.
5.7.2.1 Min-Max standardisation
In the code chunk below, normalize() of heatmaply package is used to stadardisation the clustering variables by using Min-Max method. The summary() is then used to display the summary statistics of the standardised clustering variables.
shan_ict.std <- normalize(shan_ict)
summary(shan_ict.std) RADIO_PR TV_PR LLPHONE_PR MPHONE_PR
Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
1st Qu.:0.2544 1st Qu.:0.4600 1st Qu.:0.1123 1st Qu.:0.2199
Median :0.4097 Median :0.5523 Median :0.1948 Median :0.3846
Mean :0.4199 Mean :0.5416 Mean :0.2703 Mean :0.3972
3rd Qu.:0.5330 3rd Qu.:0.6750 3rd Qu.:0.3746 3rd Qu.:0.5608
Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
COMPUTER_PR
Min. :0.00000
1st Qu.:0.09598
Median :0.17607
Mean :0.23692
3rd Qu.:0.29868
Max. :1.00000 Notice that the values range of the Min-max standardised clustering variables are 0-1 now.
5.7.2.2 Z-score standardisation
Z-score standardisation can be performed easily by using scale() of Base R. The code chunk below is used to stadardisation the clustering variables by using Z-score method.
shan_ict.z <- scale(shan_ict)
describe(shan_ict.z) vars n mean sd median trimmed mad min max range skew kurtosis
RADIO_PR 1 55 0 1 -0.04 -0.06 0.94 -1.85 2.55 4.40 0.48 -0.27
TV_PR 2 55 0 1 0.05 0.04 0.78 -2.47 2.09 4.56 -0.38 -0.23
LLPHONE_PR 3 55 0 1 -0.33 -0.15 0.68 -1.19 3.20 4.39 1.37 1.49
MPHONE_PR 4 55 0 1 -0.05 -0.06 1.01 -1.58 2.40 3.98 0.48 -0.34
COMPUTER_PR 5 55 0 1 -0.26 -0.18 0.64 -1.03 3.31 4.34 1.80 2.96
se
RADIO_PR 0.13
TV_PR 0.13
LLPHONE_PR 0.13
MPHONE_PR 0.13
COMPUTER_PR 0.13Notice the mean and standard deviation of the Z-score standardised clustering variables are 0 and 1 respectively.
5.7.2.3 Visualise the standardised clustering variables
Beside reviewing the summary statistics of the standardised clustering variables, it is also a good practice to visualise their distribution graphical.
The code chunk below plot the scaled Radio_PR field.
r <- ggplot(data=ict_derived,
aes(x= `RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue") +
ggtitle("Radio_PR without \nstandardisation") +
theme(plot.title = element_text(size=10,face="bold"))
shan_ict_s_df <- as.data.frame(shan_ict.std)
s <- ggplot(data=shan_ict_s_df,
aes(x=`RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue") +
ggtitle("Radio_PR with \nMin-Max Standardisation") +
theme(plot.title = element_text(size=10,face="bold"))
shan_ict_z_df <- as.data.frame(shan_ict.z)
z <- ggplot(data=shan_ict_z_df,
aes(x=`RADIO_PR`)) +
geom_histogram(bins=20,
color="black",
fill="light blue") +
ggtitle("Radio_PR with \nZ-score Standardisation") +
theme(plot.title = element_text(size=10,face="bold"))
ggarrange(r, s, z,
ncol = 3,
nrow = 1)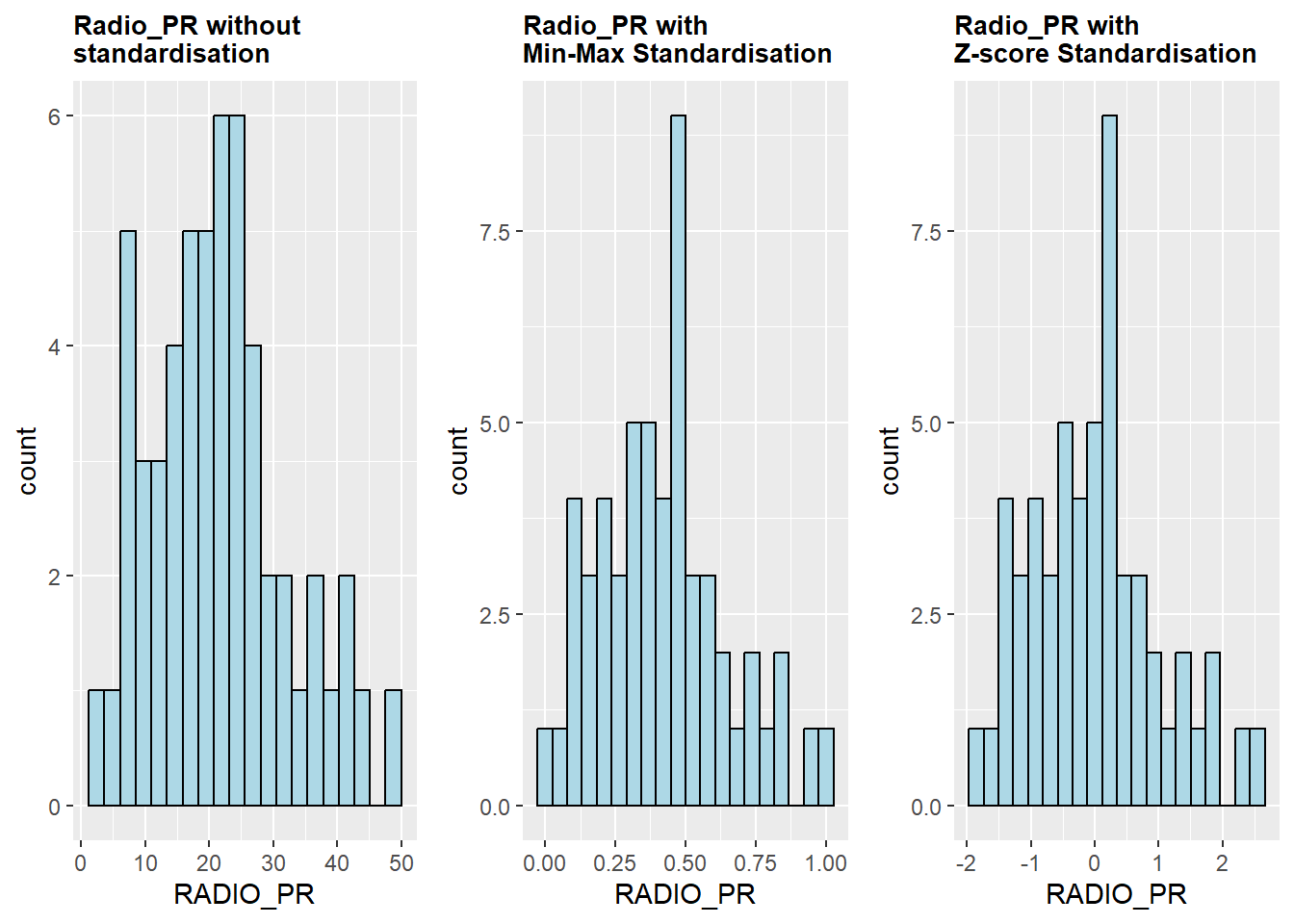
Notice that the overall distribution of the clustering variables will change after the data standardisation.
What statistical conclusion can you draw from the histograms above? Reply: Standardising the effect of making the distribution of the variable more symmetrical. |
However, it is advisable NOT to perform data standardisation if the value range of the clustering variables are not vastly different
We can plot the density curve using the following code chunk.
r <- ggplot(data=ict_derived,
aes(x= `RADIO_PR`)) +
geom_density(color="black",
fill="light blue") +
ggtitle("Raw values without \nstandardisation")
shan_ict_s_df <- as.data.frame(shan_ict.std)
s <- ggplot(data=shan_ict_s_df,
aes(x=`RADIO_PR`)) +
geom_density(color="black",
fill="light blue") +
ggtitle("Min-Max \nStandardisation")
shan_ict_z_df <- as.data.frame(shan_ict.z)
z <- ggplot(data=shan_ict_z_df,
aes(x=`RADIO_PR`)) +
geom_density(color="black",
fill="light blue") +
ggtitle("Z-score \nStandardisation")
ggarrange(r, s, z,
ncol = 3,
nrow = 1)
5.7.3 Compute proximity matrix
In R, many packages provide functions to calculate distance matrix. We will compute the proximity matrix by using dist() of R.
dist() supports six distance proximity calculations, they are: euclidean, maximum, manhattan, canberra, binary and minkowski. The default is euclidean proximity matrix.
The code chunk below is used to compute the proximity matrix using euclidean method.
proxmat <- dist(shan_ict, method = 'euclidean')The code chunk below can then be used to list the content of proxmat for visual inspection.
proxmat Mongmit Pindaya Ywangan Pinlaung Mabein Kalaw
Pindaya 17.186828
Ywangan 38.188259 25.731610
Pinlaung 5.746286 20.863519 40.005492
Mabein 26.337099 31.345776 52.914689 31.266966
Kalaw 16.005997 30.251785 49.953297 18.196406 19.814085
Pekon 5.961977 11.791580 33.650410 9.461225 28.226877 21.191531
Lawksawk 14.011550 20.432952 43.216535 19.257320 13.036525 14.001101
Nawnghkio 8.907103 18.064047 37.787702 13.927495 20.463154 12.774787
Kyaukme 14.402475 31.101487 50.589191 13.967966 26.488283 7.942225
Muse 56.301629 70.411252 89.944137 57.158335 45.327410 41.246033
Laihka 14.187227 29.861288 49.183321 10.110150 34.500222 19.734633
Mongnai 11.586190 25.849346 42.271934 6.452387 35.886053 20.034668
Mawkmai 43.492968 43.799577 39.703752 39.811227 69.324602 56.259200
Kutkai 9.761092 21.281775 36.011861 7.807733 34.055064 20.493018
Mongton 19.267961 28.335574 36.123257 16.342143 42.516902 26.787522
Mongyai 25.672744 28.741816 33.312853 22.056339 51.640426 38.674701
Mongkaing 50.361965 48.171125 36.498429 47.629056 74.717454 62.524500
Lashio 25.129457 39.898167 60.217475 26.251735 23.128227 10.669059
Mongpan 19.332063 33.572896 48.368125 19.278316 30.152942 11.469105
Matman 40.125041 35.439039 25.522031 38.240610 63.753975 53.763884
Tachileik 52.963213 63.551774 80.744220 55.501039 36.532538 37.364459
Narphan 40.615714 47.450209 45.295769 37.126895 63.034312 46.353759
Mongkhet 34.945980 39.174783 40.897731 30.586058 61.030557 46.552013
Hsipaw 11.818050 24.598884 38.863147 7.655260 36.642787 21.236711
Monghsat 21.420854 31.471506 43.298028 16.044703 47.048135 31.796188
Mongmao 24.254541 40.221719 54.285957 21.758854 38.491867 19.518913
Nansang 10.491839 27.544246 47.277637 8.549572 28.792364 12.430500
Laukkaing 56.827732 72.685355 90.882520 56.381750 52.067373 42.777791
Pangsang 27.267383 42.824958 55.682263 24.447146 41.854016 22.403998
Namtu 17.962251 22.540822 44.466868 17.004533 36.616094 30.727427
Monghpyak 17.776325 22.130579 36.744835 22.220020 21.269450 16.708436
Konkyan 40.339082 50.086933 52.812533 36.544693 61.351206 44.475859
Mongping 26.512574 31.064850 33.794020 22.975261 51.816310 37.564739
Hopong 13.693111 22.306050 35.285844 9.814855 39.800917 26.416294
Nyaungshwe 9.938590 21.652463 40.711649 13.812050 21.021337 9.566782
Hsihseng 13.149728 17.200796 34.291035 11.161846 38.120187 28.711074
Mongla 38.430076 54.942389 72.816301 37.259678 40.609124 26.026411
Hseni 18.937188 33.798982 53.444679 20.447572 21.361240 3.852842
Kunlong 22.412169 35.547066 53.163089 19.476257 39.661508 27.301375
Hopang 28.105362 44.326362 59.619312 26.596924 36.855167 18.514704
Namhkan 38.602794 54.381859 71.443173 38.278835 37.956035 24.639577
Kengtung 24.645691 38.568322 57.323173 26.348638 21.947071 8.829335
Langkho 16.426299 32.328133 50.778892 16.844228 25.384371 6.719580
Monghsu 10.915790 19.835391 34.042789 8.086834 36.719820 23.734578
Taunggyi 39.984278 50.375471 69.798323 42.954386 22.624011 25.226066
Pangwaun 38.151246 51.213162 58.013146 35.637963 52.344632 33.835194
Kyethi 20.292551 17.554012 28.729358 18.947065 44.207679 36.017247
Loilen 14.548666 29.361143 46.951621 9.156527 37.506406 21.719877
Manton 43.064070 40.242888 30.616379 40.583081 67.401120 56.016577
Mongyang 30.951302 47.593982 63.071590 28.603834 41.188352 23.356349
Kunhing 17.350424 31.823811 44.967218 14.158836 37.582140 19.763683
Mongyawng 21.421738 33.292193 57.056521 23.555497 19.349994 17.343078
Tangyan 19.592520 20.843740 32.477002 16.950567 44.859948 34.806617
Namhsan 23.778494 22.841073 28.616305 21.433352 48.833873 38.588676
Pekon Lawksawk Nawnghkio Kyaukme Muse Laihka
Pindaya
Ywangan
Pinlaung
Mabein
Kalaw
Pekon
Lawksawk 15.751129
Nawnghkio 11.315370 9.082891
Kyaukme 20.212206 18.629066 15.704230
Muse 61.456144 51.013288 53.368806 43.475768
Laihka 18.223667 24.674469 21.188187 12.824979 52.665211
Mongnai 15.160031 24.171260 18.221245 14.245669 57.197975 10.053457
Mawkmai 41.600669 56.752693 49.515047 51.202846 92.693007 42.996554
Kutkai 11.498048 22.464646 14.744053 17.093318 59.290743 14.467198
Mongton 20.814888 31.107742 22.581118 22.928509 63.471074 21.207320
Mongyai 24.252301 39.126989 31.957938 33.927780 76.391399 26.413364
Mongkaing 48.023965 62.518712 54.669447 58.605094 99.566496 52.296309
Lashio 30.380011 22.075270 23.055346 12.995255 31.315288 23.864533
Mongpan 24.330037 22.854223 17.284425 11.037831 44.749969 21.076951
Matman 36.825761 51.539711 44.405061 50.552285 92.911283 44.325453
Tachileik 57.339528 44.182621 47.045533 42.915493 22.119950 54.908985
Narphan 41.684901 52.369580 43.559661 42.030003 77.040234 39.232592
Mongkhet 34.208722 48.741102 41.410280 40.903553 81.644931 32.497428
Hsipaw 14.537542 24.935081 17.609570 16.395741 59.103355 12.842987
Monghsat 22.564279 35.231496 28.983220 25.325370 66.376026 15.893517
Mongmao 29.370625 31.464777 25.776465 14.609228 45.182530 18.599082
Nansang 16.037607 18.878869 15.113185 6.032773 48.935308 7.878999
Laukkaing 62.482399 54.883928 55.265554 42.874978 14.926996 50.739700
Pangsang 32.181214 34.591486 28.710769 17.535273 46.024292 21.419291
Namtu 16.502707 26.095300 25.752713 27.087277 65.916927 18.586794
Monghpyak 19.093173 14.231691 9.303711 21.764419 53.943485 29.322640
Konkyan 42.148797 52.031264 43.934272 39.379911 70.486973 35.175354
Mongping 25.968288 39.647081 31.614719 33.028984 74.444948 27.282761
Hopong 13.886577 27.491604 20.488286 21.884211 64.868011 15.748857
Nyaungshwe 13.931874 10.417830 4.326545 12.650414 50.588581 20.171653
Hsihseng 10.530573 25.711202 20.988026 25.027059 67.766886 17.589761
Mongla 44.120998 39.318472 38.140808 24.158966 25.680556 31.593218
Hseni 24.398001 17.150398 16.405304 8.120593 38.130567 20.449010
Kunlong 24.936301 31.830406 28.504608 21.563037 54.724297 12.268682
Hopang 33.638582 32.116462 27.984188 15.491633 37.744407 23.078652
Namhkan 44.277120 37.941126 36.733575 24.781990 23.867060 34.243665
Kengtung 29.767761 20.938215 20.829647 13.623356 33.008211 25.823950
Langkho 21.921623 19.030257 15.651662 5.167279 41.364173 16.094435
Monghsu 11.384636 24.204063 17.009168 20.077712 63.321624 16.328926
Taunggyi 44.066133 30.496838 34.479200 31.260547 25.081471 42.536916
Pangwaun 42.381347 45.302765 38.167478 30.831407 54.197887 35.178203
Kyethi 16.243575 31.774604 26.721607 32.814177 75.716745 25.583275
Loilen 18.194596 26.529318 21.926405 14.692675 56.043400 5.969478
Manton 40.382131 55.113000 47.577296 52.286003 94.149778 45.830232
Mongyang 36.358788 36.337684 32.332123 18.859489 38.959919 22.971502
Kunhing 21.346379 27.868953 20.615773 14.500266 53.300162 14.203682
Mongyawng 24.843910 17.907229 22.061209 18.155295 42.237358 21.199976
Tangyan 16.779937 32.314701 26.907880 30.678359 73.693741 22.429176
Namhsan 20.716559 36.284062 29.974967 34.785944 77.852971 27.379672
Mongnai Mawkmai Kutkai Mongton Mongyai Mongkaing
Pindaya
Ywangan
Pinlaung
Mabein
Kalaw
Pekon
Lawksawk
Nawnghkio
Kyaukme
Muse
Laihka
Mongnai
Mawkmai 37.450873
Kutkai 9.115307 36.495519
Mongton 13.167061 31.335220 10.706341
Mongyai 20.323607 17.870499 18.894166 15.979790
Mongkaing 45.600842 13.329995 42.896133 36.550032 26.284016
Lashio 27.086983 63.860773 28.982513 34.711584 46.636472 70.865819
Mongpan 17.809554 50.999632 18.518173 20.031803 34.639710 56.356780
Matman 37.633870 14.783545 34.086349 30.304574 18.695158 13.551424
Tachileik 56.395232 91.938755 56.899109 60.876740 75.029555 96.714087
Narphan 32.931700 27.375350 31.427683 21.597925 24.882845 28.565085
Mongkhet 27.576855 11.558388 27.391673 22.322828 10.498924 22.260577
Hsipaw 5.268195 35.134601 5.146282 9.069766 17.733790 42.377868
Monghsat 12.525968 27.509705 15.432012 15.098053 12.735225 37.560376
Mongmao 18.829603 48.552853 20.469232 20.657001 33.561300 55.231959
Nansang 9.279567 46.241938 13.004549 19.958124 28.855962 54.216609
Laukkaing 55.156800 88.251110 58.038112 60.466190 73.268347 95.411795
Pangsang 20.425746 48.414757 22.833583 21.077938 34.330638 54.840662
Namtu 20.935473 42.795451 22.528268 30.871751 27.802761 52.504057
Monghpyak 25.326470 53.671695 20.661627 25.804282 37.001575 56.821089
Konkyan 32.882831 33.901411 31.060810 24.825265 28.787384 38.092091
Mongping 20.299615 19.431049 18.275266 11.986993 6.538727 25.718572
Hopong 9.153795 30.284362 7.345899 10.621031 12.462791 37.937916
Nyaungshwe 16.963695 50.299026 15.215482 21.972196 32.713541 55.732112
Hsihseng 14.236728 32.929477 12.821054 19.464317 16.227126 41.159788
Mongla 35.410985 68.688950 38.840984 41.106668 53.528615 76.148327
Hseni 21.681639 58.253670 22.937894 28.675945 40.823212 64.804408
Kunlong 20.292529 44.653763 20.454010 27.002165 29.936066 53.991284
Hopang 24.300945 56.124281 26.331986 27.350305 40.873288 62.617673
Namhkan 37.005669 70.647792 39.248568 41.453594 55.062819 77.139688
Kengtung 27.228711 63.254638 27.919573 32.938387 46.039706 69.274693
Langkho 17.467678 53.108019 18.051419 23.670878 35.895672 59.742714
Monghsu 8.411238 33.207962 6.260859 10.704894 15.486049 40.071816
Taunggyi 44.855282 81.074692 45.033382 50.840925 63.594105 86.621117
Pangwaun 31.213429 50.068857 32.180465 25.750434 39.407696 53.695736
Kyethi 21.050453 27.885535 18.423422 22.252947 13.779420 35.206533
Loilen 5.841263 38.873386 13.156529 17.616001 22.479239 48.218190
Manton 39.154062 10.908779 36.182684 31.020581 19.559882 8.175337
Mongyang 26.039387 55.883162 28.533223 29.560023 41.431237 63.191325
Kunhing 11.055197 39.843973 10.884990 11.403609 23.899570 46.503971
Mongyawng 27.577546 62.004321 28.103383 37.522688 44.578964 70.098284
Tangyan 18.037471 26.266006 16.661820 19.888460 10.908506 34.856123
Namhsan 21.810003 21.519289 19.132762 19.676188 7.735900 28.866231
Lashio Mongpan Matman Tachileik Narphan Mongkhet
Pindaya
Ywangan
Pinlaung
Mabein
Kalaw
Pekon
Lawksawk
Nawnghkio
Kyaukme
Muse
Laihka
Mongnai
Mawkmai
Kutkai
Mongton
Mongyai
Mongkaing
Lashio
Mongpan 17.233279
Matman 62.811049 49.481014
Tachileik 31.195286 41.103849 89.012935
Narphan 52.563854 37.113393 31.205193 76.029566
Mongkhet 53.444463 41.217123 20.302855 82.050164 21.728718
Hsipaw 29.086435 17.952054 34.445451 57.618780 29.540170 25.380950
Monghsat 37.786793 28.330992 31.359911 67.709508 27.821548 16.798445
Mongmao 21.423677 13.159966 50.159903 47.295568 33.142618 37.535820
Nansang 18.447950 14.477393 45.806573 48.677266 39.813308 36.099219
Laukkaing 33.465738 43.558047 90.372094 32.506329 70.882887 76.906406
Pangsang 23.672516 14.023910 50.629940 48.131907 31.630314 37.558139
Namtu 36.588437 35.291394 41.665397 65.956458 49.436143 35.599713
Monghpyak 26.209281 18.785699 47.046845 44.404411 44.840651 46.263265
Konkyan 48.551312 36.587588 39.240306 73.092980 15.882353 25.424424
Mongping 45.452548 31.847482 20.165224 72.708969 18.864567 11.380917
Hopong 34.531042 23.943845 29.184351 63.245718 29.440441 21.299485
Nyaungshwe 20.158191 13.729734 46.091883 44.581335 42.794086 41.708639
Hsihseng 36.900833 29.587811 30.402806 65.887060 37.752977 25.670338
Mongla 17.995877 25.320001 70.817595 34.733155 53.146949 57.440292
Hseni 7.941836 12.066550 56.464051 35.490063 47.412297 48.188406
Kunlong 29.523103 28.803320 46.827436 59.570536 41.307823 34.168641
Hopang 17.063913 13.562913 57.355355 40.382035 39.785908 45.151070
Namhkan 17.327153 24.034131 71.542102 29.591660 53.685519 59.619944
Kengtung 5.985893 14.221554 61.301033 29.590429 50.540025 53.135998
Langkho 11.518145 9.498486 51.886151 40.233622 42.065204 42.808061
Monghsu 32.571557 21.625326 30.813805 60.502113 31.192379 24.773318
Taunggyi 19.514541 31.981385 77.845810 15.084117 68.420905 71.280752
Pangwaun 36.245608 23.252209 52.343600 54.060474 26.464997 40.702947
Kyethi 44.710266 35.889620 23.383079 72.887329 37.490376 23.325039
Loilen 26.892310 20.725000 40.656282 57.375476 35.479137 28.476895
Manton 64.666493 50.796808 5.952318 91.023039 28.026395 18.133894
Mongyang 20.933700 19.493467 58.561776 44.879027 40.139475 44.540621
Kunhing 25.510832 13.785278 40.366587 53.226397 28.162645 29.249814
Mongyawng 17.270139 27.515989 60.180824 43.210118 57.276394 52.291815
Tangyan 42.984475 34.039128 24.278233 71.984066 34.884991 20.149393
Namhsan 47.204024 36.477086 18.009747 75.403913 31.654695 17.090848
Hsipaw Monghsat Mongmao Nansang Laukkaing Pangsang
Pindaya
Ywangan
Pinlaung
Mabein
Kalaw
Pekon
Lawksawk
Nawnghkio
Kyaukme
Muse
Laihka
Mongnai
Mawkmai
Kutkai
Mongton
Mongyai
Mongkaing
Lashio
Mongpan
Matman
Tachileik
Narphan
Mongkhet
Hsipaw
Monghsat 12.178922
Mongmao 18.599483 24.717708
Nansang 12.024428 20.192690 16.499494
Laukkaing 56.906099 62.644910 40.400848 48.060074
Pangsang 20.504337 25.637933 5.760801 19.336162 40.804016
Namtu 22.944658 23.178673 36.503882 21.761884 66.406286 39.297391
Monghpyak 23.767919 35.684917 29.188846 22.752638 56.584279 31.511651
Konkyan 29.674316 26.825060 28.187425 37.470456 63.592043 27.481900
Mongping 16.892101 14.095392 30.557166 28.736626 70.813447 30.833123
Hopong 6.286179 10.045714 24.416253 16.766291 62.848557 26.151075
Nyaungshwe 16.992664 28.637238 23.045003 13.118943 52.024345 25.777823
Hsihseng 13.654610 15.349551 31.198001 19.353779 67.074564 33.552974
Mongla 37.347509 42.900536 21.624705 28.945119 20.255831 21.788123
Hseni 23.148538 33.122632 18.467099 13.645492 39.174585 21.466375
Kunlong 20.510051 20.231862 22.443391 18.301388 52.188657 25.849342
Hopang 24.872536 31.764824 7.829342 19.647091 33.167199 9.257672
Namhkan 38.279302 45.510875 22.332205 30.289487 19.646063 23.138484
Kengtung 28.408582 38.372138 20.758055 19.367980 35.148520 22.985484
Langkho 18.305109 27.952329 13.450170 9.939859 41.041270 16.765920
Monghsu 5.855724 13.724737 24.243599 15.359962 61.901766 26.052971
Taunggyi 46.231183 56.288102 38.733906 36.504897 34.598041 40.559730
Pangwaun 29.812447 34.353898 18.740057 32.612960 47.063605 15.748757
Kyethi 19.517677 19.050609 37.789657 27.302385 74.999415 39.689963
Loilen 9.804789 11.865144 19.026490 9.423028 53.557527 20.794433
Manton 35.960008 31.715603 50.379786 47.655544 90.738406 50.475214
Mongyang 26.710497 31.264797 9.106281 21.849285 32.619219 10.837735
Kunhing 9.077517 16.538834 10.391040 12.820940 50.041640 12.318870
Mongyawng 29.470967 36.440429 29.640789 19.111990 45.480044 33.616703
Tangyan 16.769794 14.459626 34.714183 24.970235 72.240954 36.476893
Namhsan 19.447928 16.956962 37.171448 29.416284 76.045960 38.565526
Namtu Monghpyak Konkyan Mongping Hopong Nyaungshwe
Pindaya
Ywangan
Pinlaung
Mabein
Kalaw
Pekon
Lawksawk
Nawnghkio
Kyaukme
Muse
Laihka
Mongnai
Mawkmai
Kutkai
Mongton
Mongyai
Mongkaing
Lashio
Mongpan
Matman
Tachileik
Narphan
Mongkhet
Hsipaw
Monghsat
Mongmao
Nansang
Laukkaing
Pangsang
Namtu
Monghpyak 34.657799
Konkyan 47.837690 46.339594
Mongping 32.166441 35.476537 24.202901
Hopong 20.682668 26.795563 30.449287 13.400139
Nyaungshwe 27.141464 10.397300 43.235040 31.932583 20.932532
Hsihseng 13.189940 28.537627 38.349700 19.964389 9.165458 22.580242
Mongla 48.349434 40.803397 46.809747 51.261580 43.231105 34.760273
Hseni 32.741448 20.026876 44.884563 39.558453 28.641193 13.086310
Kunlong 23.360474 35.744661 32.911433 30.905385 21.906817 28.513095
Hopang 40.824516 30.426577 34.818522 37.927212 30.977356 24.719891
Namhkan 50.632466 37.950202 48.159596 52.374815 44.413246 33.332428
Kengtung 38.533554 22.147613 47.482621 44.280821 34.047382 17.775714
Langkho 30.503473 20.027496 38.695022 34.396455 23.963685 12.826577
Monghsu 20.964684 23.217823 33.172187 15.890478 4.340665 17.382799
Taunggyi 51.872748 33.417439 65.056905 62.153039 51.376415 32.509619
Pangwaun 51.703554 38.195144 26.397576 34.037881 34.600673 35.292324
Kyethi 18.690932 32.816234 40.010989 18.743974 13.649038 28.806872
Loilen 19.424075 29.699681 33.419820 23.199959 12.474445 20.640432
Manton 44.858230 50.220840 36.666876 20.048082 31.058885 48.879874
Mongyang 41.326052 35.817599 32.939338 38.780686 32.335704 29.429500
Kunhing 29.643996 25.074435 25.374202 21.259619 14.515617 18.997131
Mongyawng 26.224331 28.556475 52.238580 45.559190 32.659925 21.812104
Tangyan 17.869483 33.526416 36.746064 16.167411 10.682328 28.414692
Namhsan 24.095555 35.270492 35.220115 13.023777 13.270541 31.591750
Hsihseng Mongla Hseni Kunlong Hopang Namhkan
Pindaya
Ywangan
Pinlaung
Mabein
Kalaw
Pekon
Lawksawk
Nawnghkio
Kyaukme
Muse
Laihka
Mongnai
Mawkmai
Kutkai
Mongton
Mongyai
Mongkaing
Lashio
Mongpan
Matman
Tachileik
Narphan
Mongkhet
Hsipaw
Monghsat
Mongmao
Nansang
Laukkaing
Pangsang
Namtu
Monghpyak
Konkyan
Mongping
Hopong
Nyaungshwe
Hsihseng
Mongla 47.866210
Hseni 31.274375 22.682048
Kunlong 23.185967 34.646200 27.619175
Hopang 37.001334 14.702444 16.280878 27.134451
Namhkan 49.209476 7.721355 21.211323 37.573885 14.618632
Kengtung 37.072441 20.245004 6.612817 31.714187 16.429921 17.563015
Langkho 27.627441 22.901675 6.666133 22.452741 13.424847 22.440029
Monghsu 9.782470 42.451868 26.228462 23.989665 30.184458 43.132637
Taunggyi 52.814240 29.709863 23.819389 47.129032 32.995252 25.729147
Pangwaun 43.306326 31.918643 33.070182 39.245403 20.698364 31.044067
Kyethi 8.404049 55.602500 38.833498 29.855859 44.048114 56.786202
Loilen 15.884853 33.867408 22.710984 16.653599 24.289326 36.490647
Manton 33.487758 71.251416 58.463341 47.976855 57.752046 72.186149
Mongyang 38.259743 14.666661 21.019929 24.722785 6.925859 16.772448
Kunhing 22.015490 30.647566 20.647448 19.377551 17.296164 31.492119
Mongyawng 30.951462 31.557550 17.386004 24.039800 29.051360 32.121112
Tangyan 7.027241 52.680849 37.307575 26.807983 41.222167 54.264078
Namhsan 12.574240 56.402740 41.196125 31.040560 44.051555 57.642717
Kengtung Langkho Monghsu Taunggyi Pangwaun Kyethi
Pindaya
Ywangan
Pinlaung
Mabein
Kalaw
Pekon
Lawksawk
Nawnghkio
Kyaukme
Muse
Laihka
Mongnai
Mawkmai
Kutkai
Mongton
Mongyai
Mongkaing
Lashio
Mongpan
Matman
Tachileik
Narphan
Mongkhet
Hsipaw
Monghsat
Mongmao
Nansang
Laukkaing
Pangsang
Namtu
Monghpyak
Konkyan
Mongping
Hopong
Nyaungshwe
Hsihseng
Mongla
Hseni
Kunlong
Hopang
Namhkan
Kengtung
Langkho 10.716213
Monghsu 31.691914 22.184918
Taunggyi 18.628225 28.827478 48.691951
Pangwaun 33.748335 29.538434 34.338498 49.761245
Kyethi 44.426274 35.091512 14.661572 59.957407 47.662610
Loilen 28.222935 18.410672 13.155208 45.591617 33.169981 23.232965
Manton 63.199123 53.595620 33.076503 80.308034 51.079265 27.203299
Mongyang 21.708047 17.535413 32.395988 37.458247 22.525026 45.386726
Kunhing 24.595083 14.638284 14.678891 42.998509 22.909986 27.895182
Mongyawng 20.387199 18.611584 31.285089 28.773864 47.533116 38.771518
Tangyan 42.995076 33.202048 12.742203 59.265262 44.705580 4.779331
Namhsan 46.620497 36.820978 15.322576 63.149232 44.858030 6.867929
Loilen Manton Mongyang Kunhing Mongyawng Tangyan
Pindaya
Ywangan
Pinlaung
Mabein
Kalaw
Pekon
Lawksawk
Nawnghkio
Kyaukme
Muse
Laihka
Mongnai
Mawkmai
Kutkai
Mongton
Mongyai
Mongkaing
Lashio
Mongpan
Matman
Tachileik
Narphan
Mongkhet
Hsipaw
Monghsat
Mongmao
Nansang
Laukkaing
Pangsang
Namtu
Monghpyak
Konkyan
Mongping
Hopong
Nyaungshwe
Hsihseng
Mongla
Hseni
Kunlong
Hopang
Namhkan
Kengtung
Langkho
Monghsu
Taunggyi
Pangwaun
Kyethi
Loilen
Manton 41.906087
Mongyang 24.676592 58.570558
Kunhing 13.039336 41.049230 18.889405
Mongyawng 26.175211 62.943339 30.421734 29.535984
Tangyan 19.660826 27.182672 42.106366 24.974161 37.752279
Namhsan 24.215271 21.048485 45.097869 27.079121 43.002019 6.3676135.7.4 Computing hierarchical clustering
In R, there are several packages which provide hierarchical clustering function. In this hands-on exercise, hclust() of R stats will be used.
hclust() employs agglomeration method to compute the cluster. Eight clustering algorithms are supported, they are: (i) ward.D, (ii) ward.D2, (iii) single, (iv) complete, (v) average(UPGMA), (vi) mcquitty(WPGMA), (vii) median(WPGMC) and (viii) centroid(UPGMC).
The code chunk below performs hierarchical cluster analysis using ward.D method. The hierarchical clustering output is stored in an object of class hclust which contains the tree produced by the clustering process.
hclust_ward <- hclust(proxmat, method = 'ward.D')We can then plot the tree by using plot() of R Graphics as shown in the code chunk below.
plot(hclust_ward, cex = 0.6)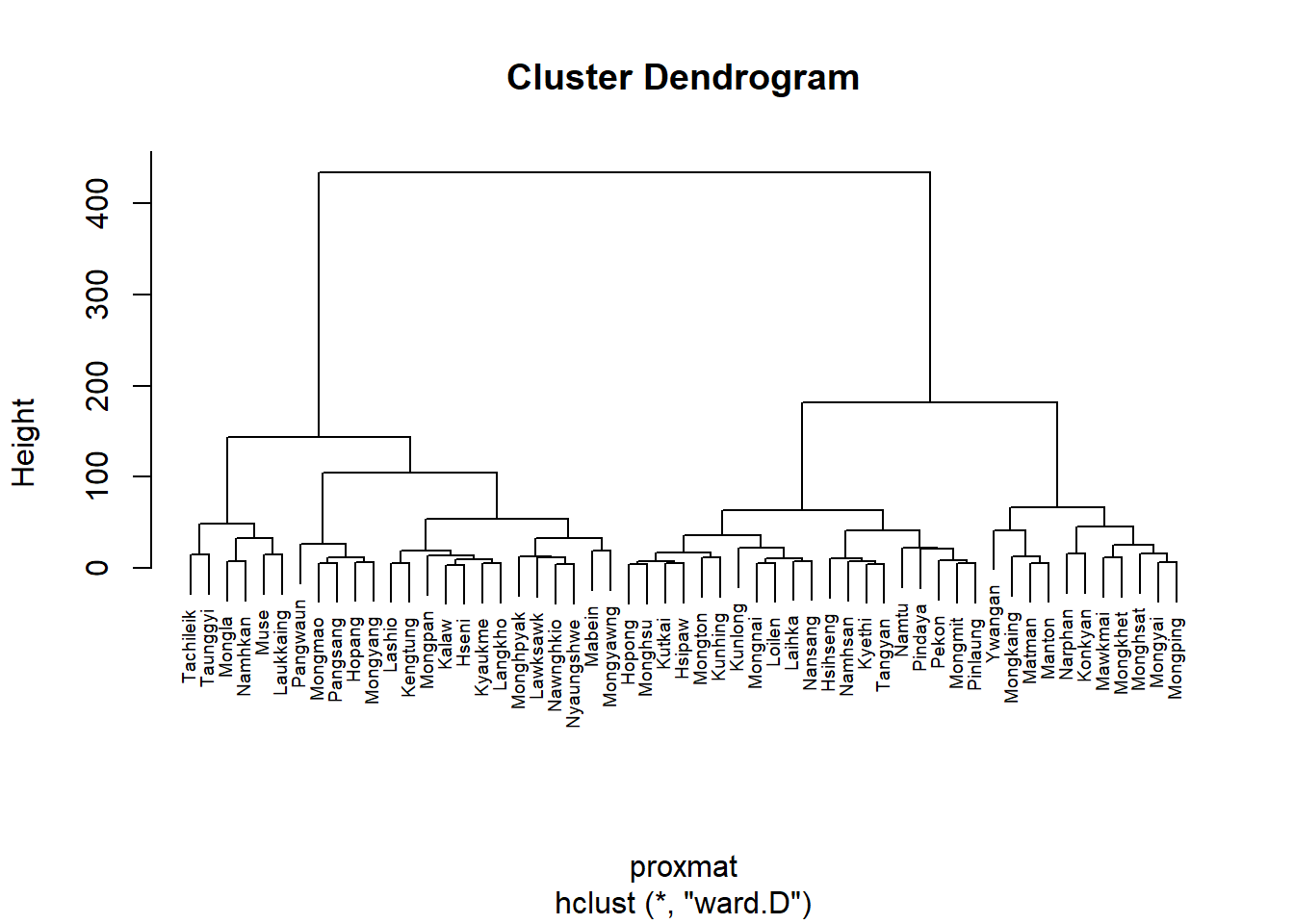
# cex is to scale down the plot to 60%, to prevent the township labels from overlapping5.7.5 Selecting the optimal clustering algorithm
One of the challenge in performing hierarchical clustering is to identify stronger clustering structures. The issue can be solved by using use agnes() function of cluster package. It functions like hclus(), however, with the agnes() function you can also get the agglomerative coefficient, which measures the amount of clustering structure found (values closer to 1 suggest strong clustering structure) by comparing the homogeneity within the clusters .
The code chunk below will be used to compute the agglomerative coefficients of 4 hierarchical clustering algorithms.
m <- c( "average", "single", "complete", "ward")
names(m) <- c( "average", "single", "complete", "ward")
ac <- function(x) {
agnes(shan_ict, method = x)$ac
}
map_dbl(m, ac) average single complete ward
0.8131144 0.6628705 0.8950702 0.9427730 From the output above, we can see that Ward’s method provides the strongest clustering structure among the four methods assessed. Hence, in the subsequent analysis, only Ward’s method will be used.
5.7.6 Determine the Optimal Clusters
Another technical challenge face by data analyst in performing clustering analysis is to determine the optimal clusters to retain.
There are three commonly used methods to determine the optimal clusters, they are:
5.7.6.1 Gap Statistic Method
The gap statistic compares the total within intra-cluster variation for different values of k with their expected values under null reference distribution of the data. The estimate of the optimal clusters will be value that maximize the gap statistic (i.e., that yields the largest gap statistic). This means that the clustering structure is far away from the random uniform distribution of points.
To compute the gap statistic, clusGap() of cluster package will be used.
set.seed(12345)
gap_stat <- clusGap(shan_ict,
FUN = hcut,
nstart = 25,
K.max = 10,
B = 50)
# K.max refers to the maximum number of clusters to consider, must be at least two.
# B refers to integer, number of Monte Carlo (“bootstrap”) samples.
# Print the result
print(gap_stat, method = "firstmax")Clustering Gap statistic ["clusGap"] from call:
clusGap(x = shan_ict, FUNcluster = hcut, K.max = 10, B = 50, nstart = 25)
B=50 simulated reference sets, k = 1..10; spaceH0="scaledPCA"
--> Number of clusters (method 'firstmax'): 1
logW E.logW gap SE.sim
[1,] 6.104544 6.378209 0.2736651 0.04460994
[2,] 5.827444 6.048127 0.2206824 0.03880130
[3,] 5.689680 5.899965 0.2102844 0.03362652
[4,] 5.559639 5.778070 0.2184311 0.03784781
[5,] 5.453876 5.675437 0.2215615 0.03897071
[6,] 5.363009 5.585192 0.2221833 0.03973087
[7,] 5.288334 5.503748 0.2154145 0.04054939
[8,] 5.224095 5.429034 0.2049390 0.04198644
[9,] 5.155439 5.358210 0.2027705 0.04421874
[10,] 5.074827 5.291273 0.2164465 0.04540947Also note that the hcut() function used is from factoextra package.
Next, we can visualise the plot by using fviz_gap_stat() of factoextra package.
fviz_gap_stat(gap_stat)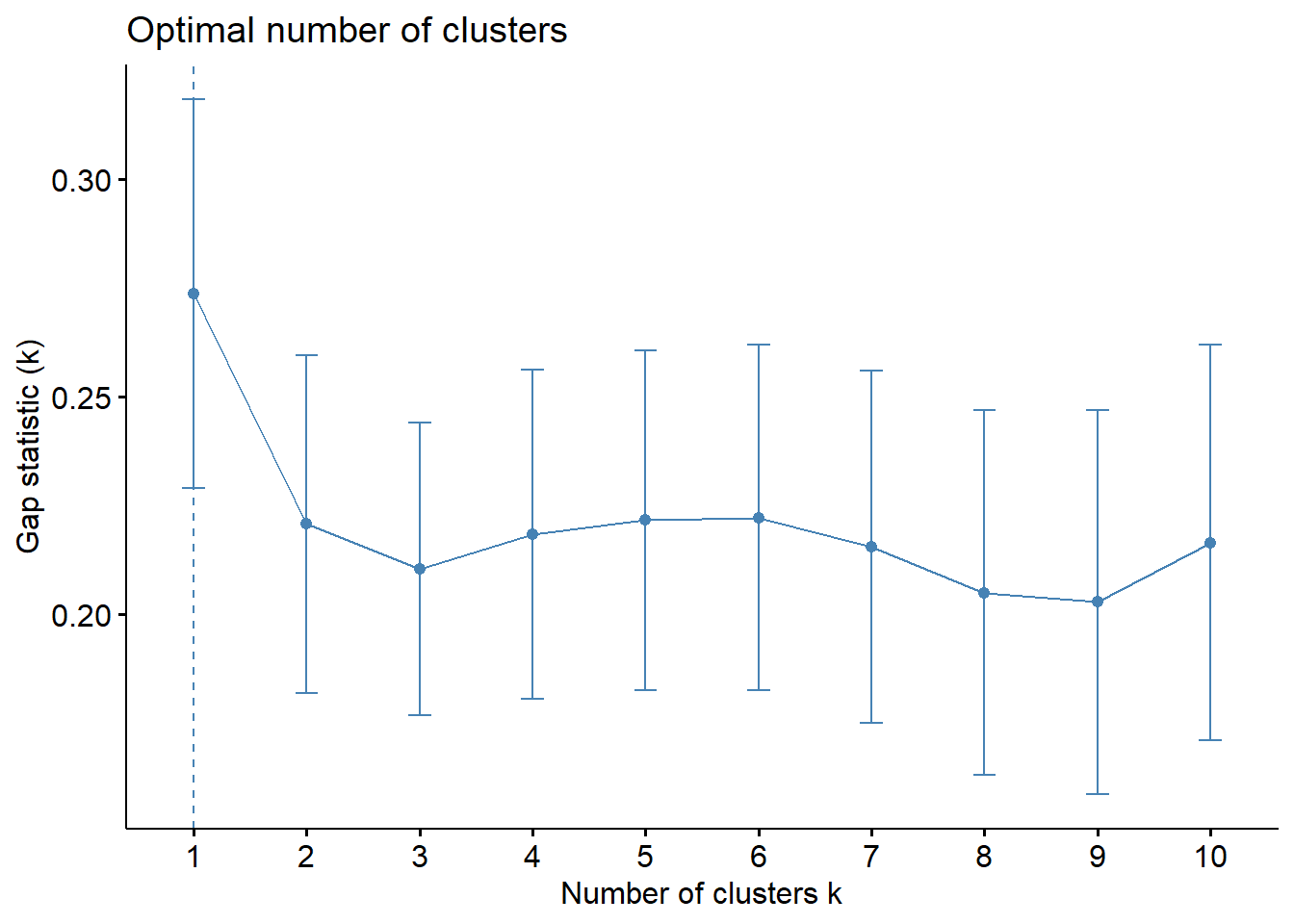
From the gap statistic graph above, the recommended number of cluster to retain is 1 or 2. However, it is not logical to retain only one or 2 clusters. Ideally, we should have 3 or more clusters. By examining the gap statistic graph, the 6-cluster gives the next largest gap statistic and should be the next best cluster number to pick.
5.7.7 Interpret the dendrograms
In the dendrogram displayed above, each leaf corresponds to one observation. As we move up the tree, observations that are similar to each other are combined into branches, which are themselves fused at a higher height.
The height of the fusion, provided on the vertical axis, indicates the (dis)similarity between two observations. The higher the height of the fusion, the less similar the observations are. Note that, conclusions about the proximity of two observations can be drawn only based on the height where branches containing those two observations first are fused. We cannot use the proximity of two observations along the horizontal axis as a criteria for their similarity.
It’s also possible to draw the dendrogram with a border around the selected clusters by using rect.hclust() of R stats. The argument border is used to specify the border colors for the rectangles.
plot(hclust_ward, cex = 0.6)
# rect is to set the rectangles
rect.hclust(hclust_ward,
k = 6,
border = 2:7)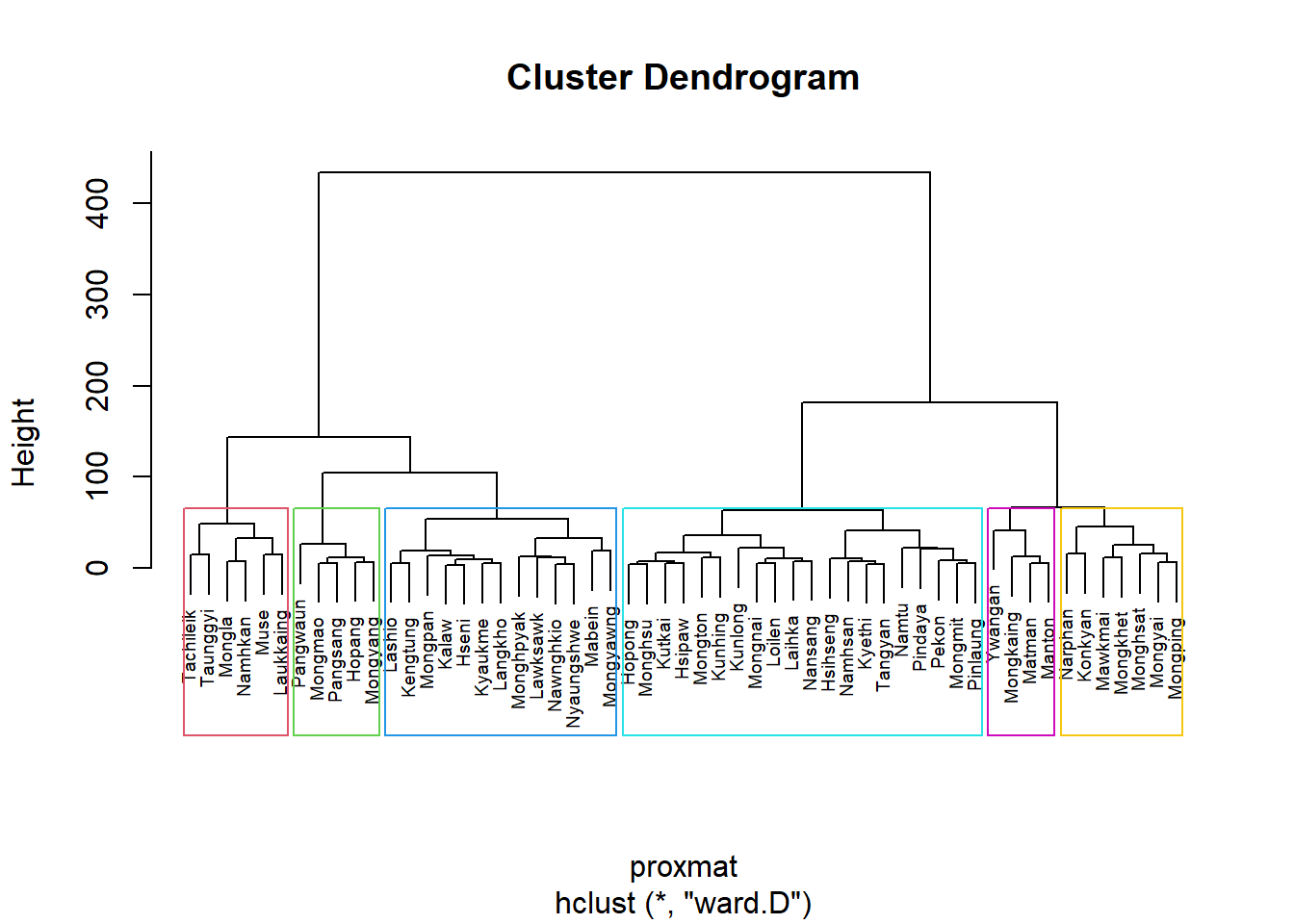
5.7.8 Visually-driven hierarchical clustering analysis
In this section, we learn how to perform visually-driven hiearchical clustering analysis by using heatmaply package.
With heatmaply, we are able to build both highly interactive cluster heatmap or static cluster heatmap.
5.7.8.1 Transforming the data frame into a matrix
The shan_ict data is currently loaded in a data frame.
The code chunk below is used to transform shan_ict data frame into a data matrix to generate the heatmap.
shan_ict_mat <- data.matrix(shan_ict)5.7.8.2 Plot interactive cluster heatmap using heatmaply()
In the code chunk below, the heatmaply() of heatmaply package is used to build an interactive cluster heatmap.
heatmaply(normalize(shan_ict_mat),
Colv=NA,
dist_method = "euclidean",
hclust_method = "ward.D",
seriate = "OLO",
colors = Blues,
k_row = 6,
margins = c(NA,200,60,NA),
fontsize_row = 5,
fontsize_col = 5,
main="Geographic Segmentation of Shan State by ICT indicators",
xlab = "ICT Indicators",
ylab = "Townships of Shan State"
)5.7.9 Map the clusters formed
With closed examination of the dendragram above, we have decided to retain six clusters.
cutree() of R Base will be used in the code chunk below to derive a 6-cluster model.
groups <- as.factor(cutree(hclust_ward, k=6))The output is called groups. It is a list object.
In order to visualise the clusters, the groups object need to be appended onto shan_sf simple feature object.
The code chunk below form the join in three steps:
the groups list object will be converted into a matrix;
cbind()is used to append groups matrix onto shan_sf to produce an output simple feature object calledshan_sf_cluster; andrename()of dplyr package is used to rename as.matrix.groups field as CLUSTER.
shan_sf_cluster <- cbind(shan_sf, as.matrix(groups)) %>%
rename(`CLUSTER`=`as.matrix.groups.`)Next, qtm() of tmap package is used to plot the choropleth map showing the cluster formed.
qtm(shan_sf_cluster, "CLUSTER") +
tm_layout(main.title = "Hierarchical Cluster Map",
main.title.position = "center",
main.title.size = 1.2)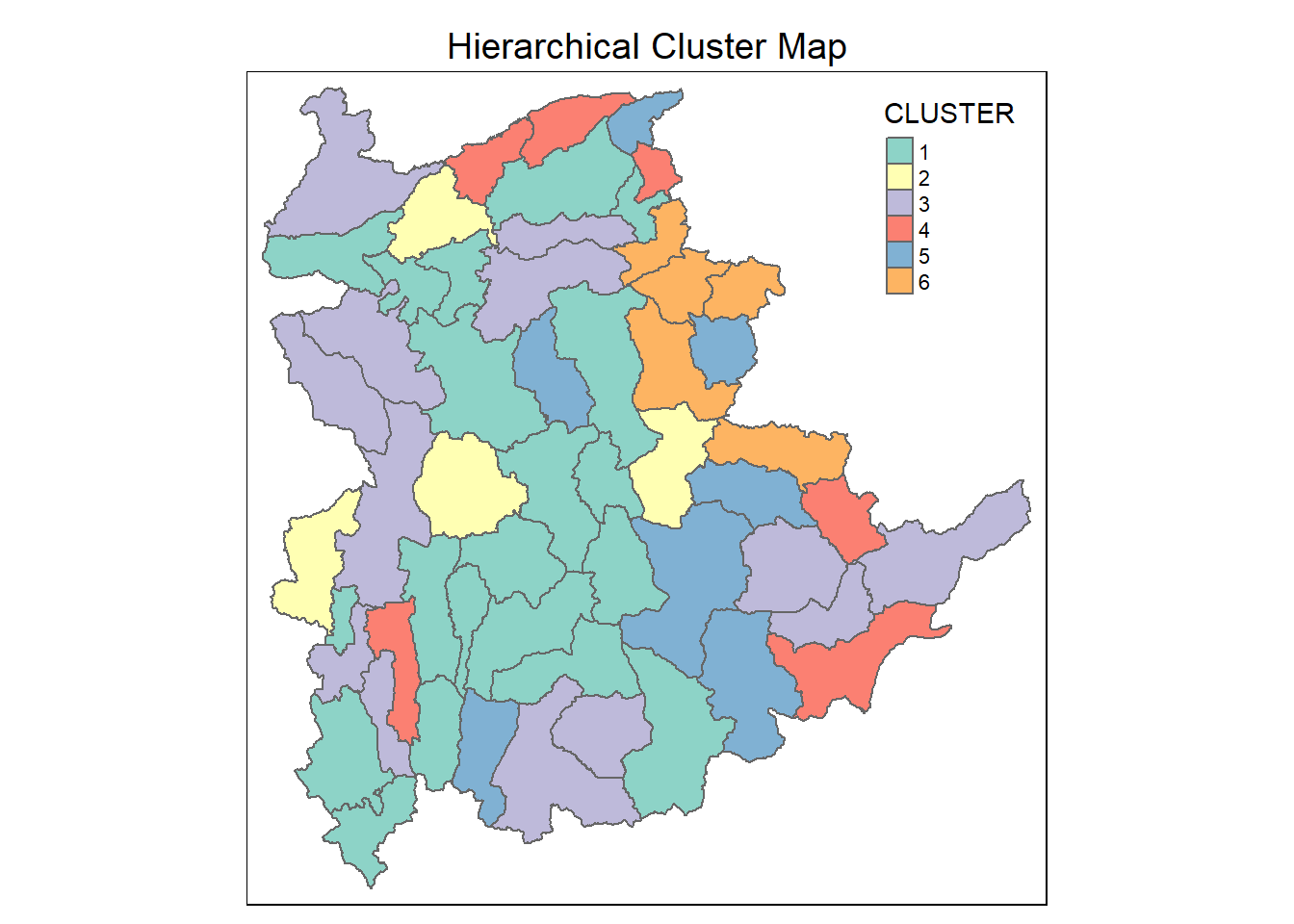
The choropleth map above reveals the clusters are very fragmented. The is one of the major limitation when non-spatial clustering algorithm such as hierarchical cluster analysis method is used.
5.8 Spatially Constrained Clustering - SKATER approach
In this section, we learn how to derive spatially constrained cluster by using skater() method of spdep package.
5.8.1 Converting into SpatialPolygonsDataFrame
First, we need to convert shan_sf into SpatialPolygonsDataFrame. This is because SKATER function only support sp objects such as SpatialPolygonDataFrame.
The code chunk below uses as_Spatial() of sf package to convert shan_sf into a SpatialPolygonDataFrame called shan_sp.
shan_sp <- as_Spatial(shan_sf)5.8.2 Computing Neighbour List
Next, poly2nd() of spdep package will be used to compute the neighbours list from polygon list.
shan.nb <- poly2nb(shan_sp, queen = TRUE)
summary(shan.nb)Neighbour list object:
Number of regions: 55
Number of nonzero links: 264
Percentage nonzero weights: 8.727273
Average number of links: 4.8
Link number distribution:
2 3 4 5 6 7 8 9
5 9 7 21 4 3 5 1
5 least connected regions:
3 5 7 9 47 with 2 links
1 most connected region:
8 with 9 linksWe plot the neighbors list on shan_sp by using the code chunk below. Since we now can plot the community area boundaries as well, we plot this graph on top of the map. The first plot command gives the boundaries. This is followed by the plot of the neighbor list object, with coordinates applied to the original SpatialPolygonDataFrame (Shan state township boundaries) to extract the centroids of the polygons. These are used as the nodes for the graph representation. We also set the color to blue and specify add=TRUE to plot the network on top of the boundaries.
plot(shan_sp,
border=grey(.5))
plot(shan.nb,
coordinates(shan_sp),
col="blue",
add=TRUE)
title(main="Neighbor Network (Queen Contiguity)")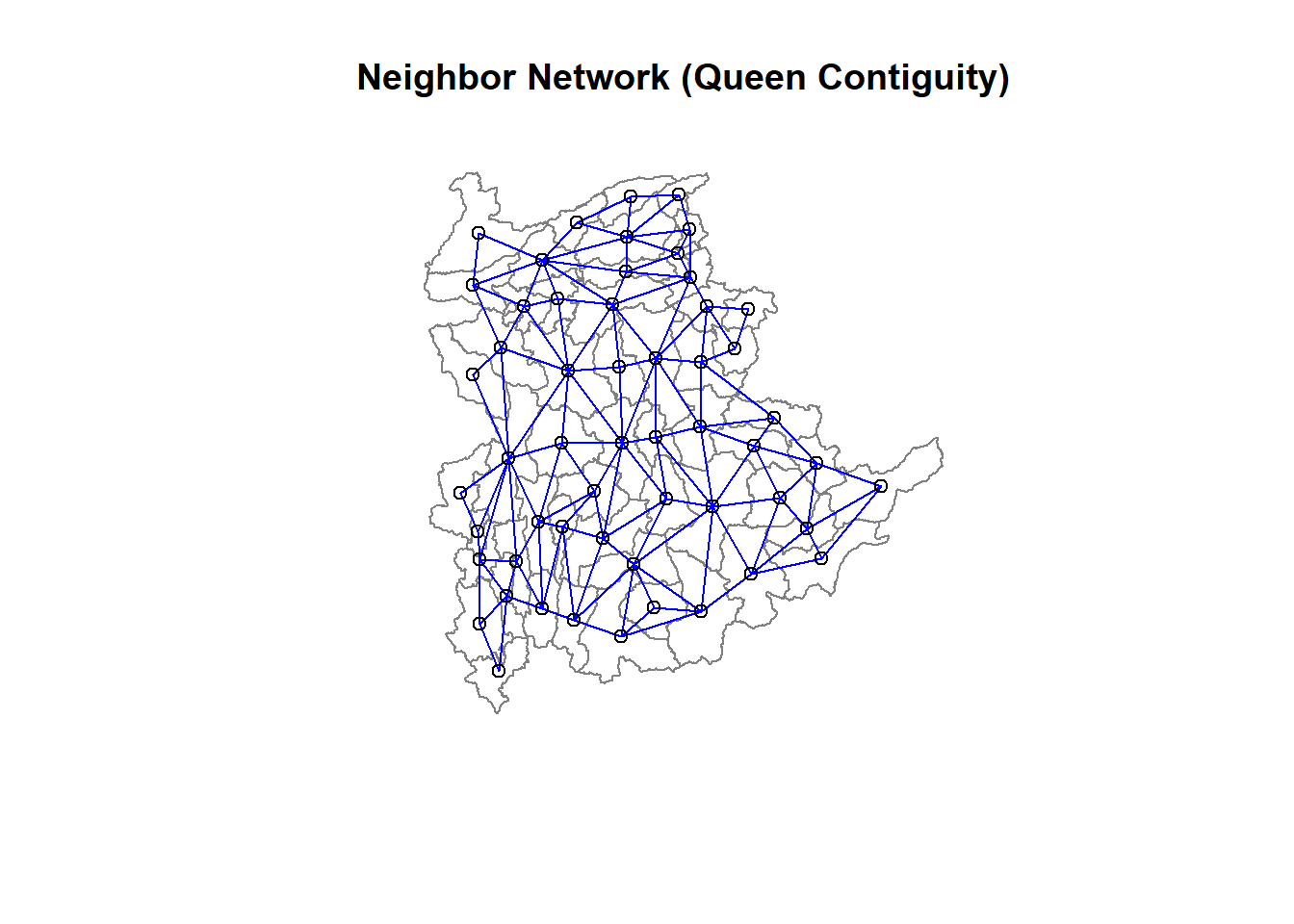
5.8.3 Compute Minimum Spanning Tree (MST)
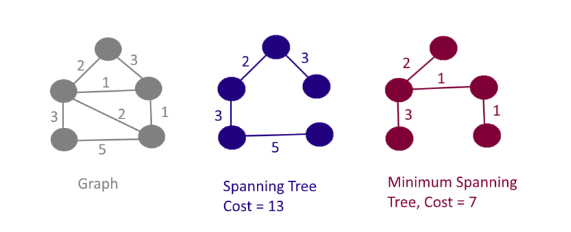
The MST is a graph that includes all the nodes in the network, but passes through each only once. So, it reduces the complexity of the original graph to one where each node is connected to only one other node. The resulting tree has n nodes and n-1 edges. The “minimum” part pertains to a cost function that is minimized. The objective is to minimize the overall length (or cost) of the tree. In its simplest form, the cost consists of the distances between the nodes. Here, however, a more general measure of cost is used in the form of the multivariate dissimilarity measure between each pair of nodes. This is based on a multivariate Euclidean distance between the standardized values for the variables, as was the case in the other clustering algorithms.
5.8.3.1 Calculate edge costs
The first step in the process is to compute the costs associated with each edge in the neighbor list. In other words, for each observation, the dissimilarity is computed between it and each of its neighbors (as defined by the neighbor list). In the spdep package, this is carried out by the nbcosts function. Its arguments are the neighbor list and the standardized data frame.
Next, nbcosts() of spdep package is used to compute the cost of each edge. It is the distance between 2 nodes, with reference to the provided attributes (in shan_ict). This function compute this distance using a data.frame with observations vector in each node.
The code chunk below is used to compute the cost of each edge.
lcosts <- nbcosts(shan.nb, shan_ict)For each observation, this gives the pairwise dissimilarity between its values on the five variables and the values for the neighbouring observation (from the neighbour list). Basically, this is the notion of a generalised weight for a spatial weights matrix.
Next, We will incorporate these costs into a weights object in the same way as we did in the calculation of inverse of distance weights. In other words, we convert the neighbour list to a list weights object by specifying the just computed lcosts as the weights.
In order to achieve this, nb2listw() of spdep package is used as shown in the code chunk below.
Note that we specify the style as B to make sure the cost values are not row-standardised.
shan.w <- nb2listw(shan.nb,
lcosts,
style="B")
summary(shan.w)Characteristics of weights list object:
Neighbour list object:
Number of regions: 55
Number of nonzero links: 264
Percentage nonzero weights: 8.727273
Average number of links: 4.8
Link number distribution:
2 3 4 5 6 7 8 9
5 9 7 21 4 3 5 1
5 least connected regions:
3 5 7 9 47 with 2 links
1 most connected region:
8 with 9 links
Weights style: B
Weights constants summary:
n nn S0 S1 S2
B 55 3025 7626.765 582607.8 52201605.8.4 Compute the minimum spanning tree
The minimum spanning tree is computed by mean of the mstree() of spdep package as shown in the code chunk below. The only required argument is the weights object. It summarizes the tree by giving each edge as the pair of connected nodes, followed by the cost associated with that edge.
shan.mst <- mstree(shan.w)After computing the MST, we can check its class and dimension by using the code chunk below.
class(shan.mst)[1] "mst" "matrix"dim(shan.mst)[1] 54 3Note that the dimension is 54 and not 55. This is because the minimum spanning tree consists on n-1 edges (links) in order to traverse all the nodes.
We can display the content of shan.mst by using head() as shown in the code chunk below.
head(shan.mst) [,1] [,2] [,3]
[1,] 31 25 22.944658
[2,] 25 10 16.395741
[3,] 10 1 14.402475
[4,] 10 9 15.704230
[5,] 9 8 9.082891
[6,] 8 6 14.001101The plot method for the MST includes a way to show the observation numbers of the nodes in addition to the edge. As before, we plot this together with the township boundaries. We can see how the initial neighbor list is simplified to just one edge connecting each of the nodes, while passing through all the nodes.
plot(shan_sp, border=gray(.5))
plot.mst(shan.mst,
coordinates(shan_sp),
col="blue",
cex.lab=0.7,
cex.circles=0.005,
add=TRUE)
title(main="Minimum Spanning Tree plot")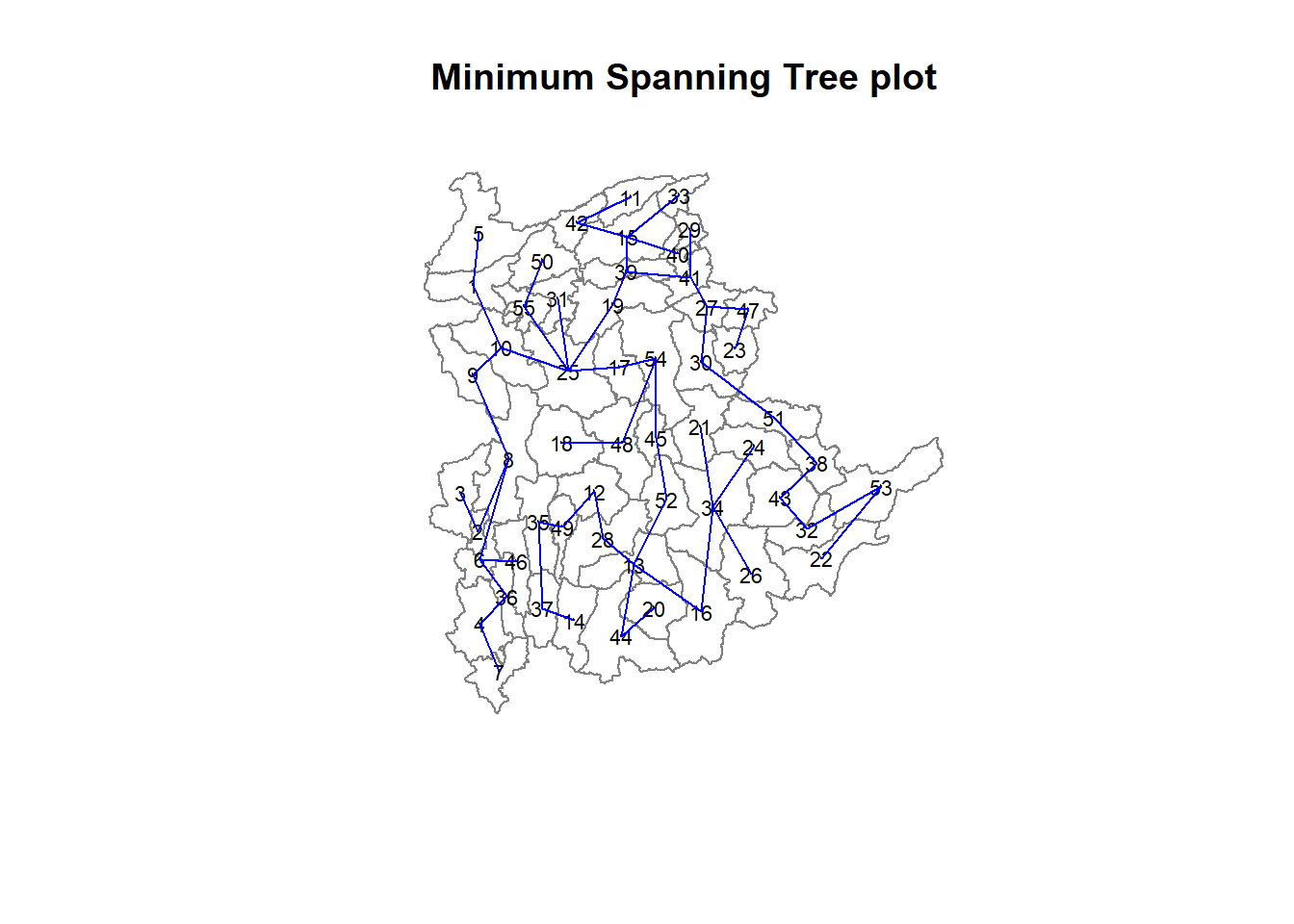
5.8.5 Compute spatially constrained clusters using SKATER method
The code chunk below computes the spatially constrained cluster using skater() of spdep package.
clust6 <- skater(edges = shan.mst[,1:2],
data = shan_ict,
method = "euclidean",
ncuts = 5)The skater() takes three mandatory arguments: -
The first two columns of the MST matrix (i.e. not the cost),
The data matrix (to update the costs as units are being grouped), and
The number of cuts.
Note: The number of cuts is set to one less than the number of clusters. So, the value specified is not the number of clusters, but the number of cuts in the graph, one less than the number of clusters.
The result of the skater() is an object of class skater. We can examine its contents by using the code chunk below.
str(clust6)List of 8
$ groups : num [1:55] 3 3 6 3 3 3 3 3 3 3 ...
$ edges.groups:List of 6
..$ :List of 3
.. ..$ node: num [1:22] 13 48 54 55 45 37 34 16 25 31 ...
.. ..$ edge: num [1:21, 1:3] 48 55 54 37 34 16 45 31 13 13 ...
.. ..$ ssw : num 342
..$ :List of 3
.. ..$ node: num [1:18] 47 27 53 38 42 15 41 51 43 32 ...
.. ..$ edge: num [1:17, 1:3] 53 15 42 38 41 51 15 27 15 43 ...
.. ..$ ssw : num 376
..$ :List of 3
.. ..$ node: num [1:11] 2 6 8 1 36 4 10 9 46 5 ...
.. ..$ edge: num [1:10, 1:3] 6 1 8 36 4 6 8 10 10 9 ...
.. ..$ ssw : num 146
..$ :List of 3
.. ..$ node: num [1:2] 44 20
.. ..$ edge: num [1, 1:3] 44 20 9.5
.. ..$ ssw : num 9.5
..$ :List of 3
.. ..$ node: num 23
.. ..$ edge: num[0 , 1:3]
.. ..$ ssw : num 0
..$ :List of 3
.. ..$ node: num 3
.. ..$ edge: num[0 , 1:3]
.. ..$ ssw : num 0
$ not.prune : NULL
$ candidates : int [1:6] 1 2 3 4 5 6
$ ssto : num 1261
$ ssw : num [1:6] 1261 1098 996 954 912 ...
$ crit : num [1:2] 1 Inf
$ vec.crit : num [1:55] 1 1 1 1 1 1 1 1 1 1 ...
- attr(*, "class")= chr "skater"The most interesting component of this list structure is the groups vector that contains the labels of the cluster to which each observation belongs (as before, the label itself is arbitrary). This is followed by a detailed summary for each cluster in the edges.groups list. Sum of squares measures are given as ssto for the total and ssw to show the effect of each cut on the overall criterion.
We can check the cluster assignment by using the code chunk below.
ccs6 <- clust6$groups
ccs6 [1] 3 3 6 3 3 3 3 3 3 3 2 1 1 1 2 1 1 1 2 4 1 2 5 1 1 1 2 1 2 2 1 2 2 1 1 3 1 2
[39] 2 2 2 2 2 4 1 3 2 1 1 1 2 1 2 1 1We can find out how many observations are in each cluster by means of the table command.
table(ccs6)ccs6
1 2 3 4 5 6
22 18 11 2 1 1 Lastly, we can also plot the pruned tree that shows the six clusters on top of the townshop area.
plot(shan_sp, border=gray(.5))
plot(clust6,
coordinates(shan_sp),
cex.lab=.7,
groups.colors=c("red","green","blue", "brown", "pink"),
cex.circles=0.005,
add=TRUE)
title(main="Minimum Spanning Tree plot \n using Skater method", add=TRUE)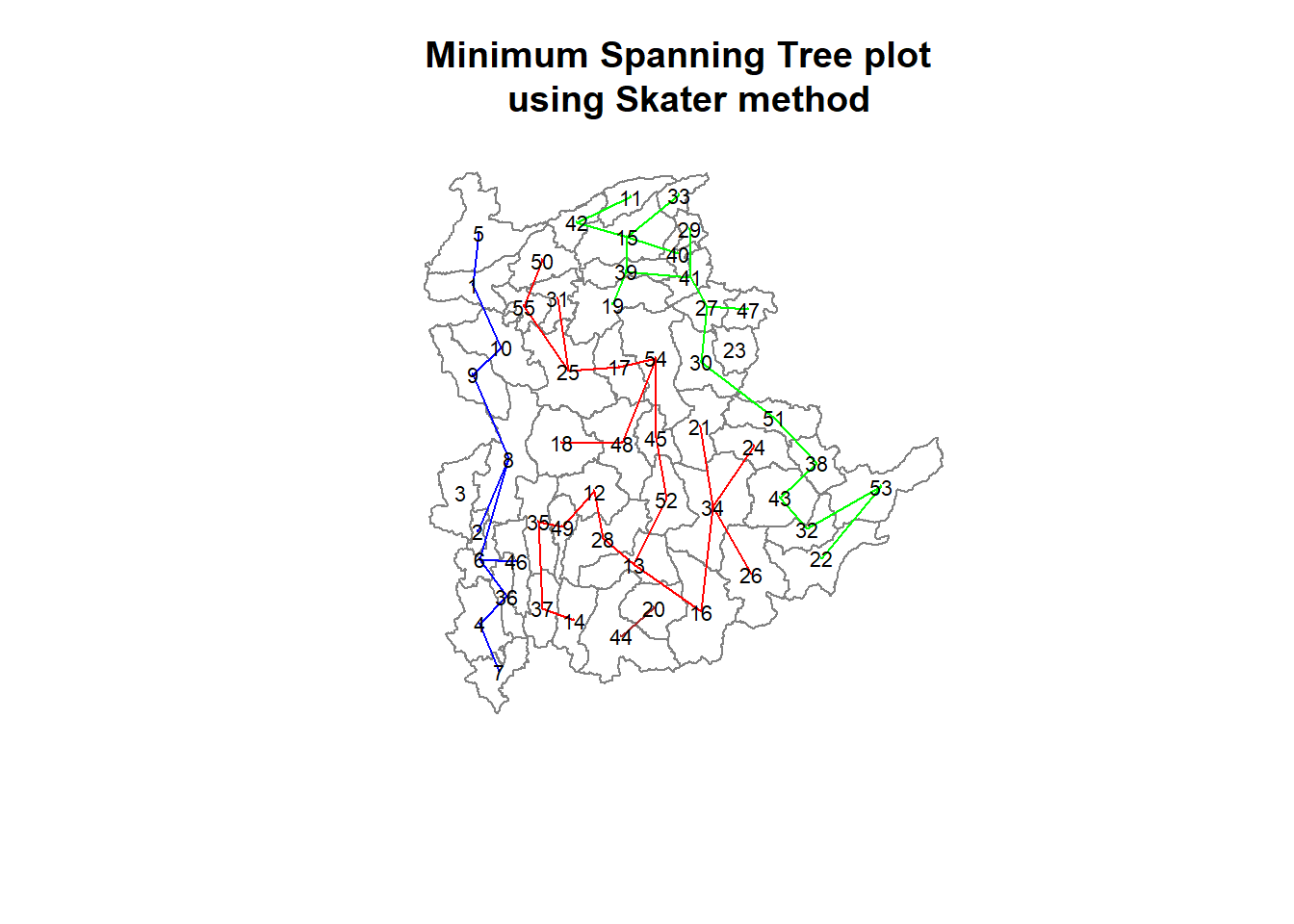
5.8.6 Visualise the clusters in choropleth map
The code chunk below is used to plot the newly derived clusters by using SKATER method.
groups_mat <- as.matrix(clust6$groups)
# Join back to the sf data table for plotting. One pre-condition for just a combination is that we must not sort the dataframe in the earlier steps
shan_sf_spatialcluster <- cbind(shan_sf_cluster, as.factor(groups_mat)) %>%
rename(`SP_CLUSTER`=`as.factor.groups_mat.`)
qtm(shan_sf_spatialcluster, "SP_CLUSTER") +
tm_layout(main.title = "Hierarchical Cluster Map \nusing Skater method",
main.title.position = "center",
main.title.size = 1.2) 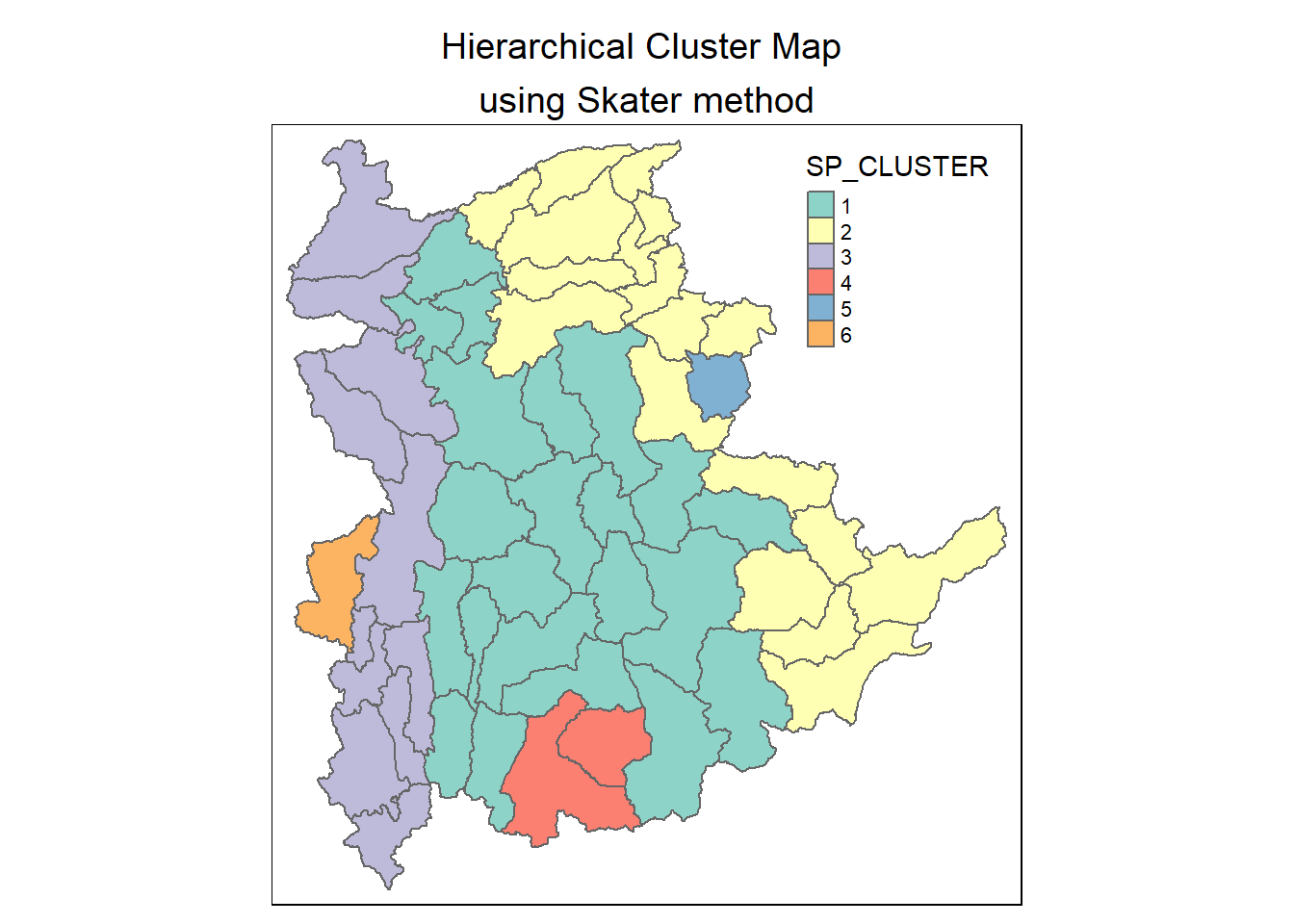
For easy comparison, it will be better to place both the hierarchical clustering and spatially constrained hierarchical clustering maps next to each other.
hclust.map <- qtm(shan_sf_cluster,
"CLUSTER") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "Hierarchical Cluster Map \n ",
main.title.position = "center",
main.title.size = 1.2)
shclust.map <- qtm(shan_sf_spatialcluster,
"SP_CLUSTER") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "Hierarchical Cluster Map \nusing Skater method",
main.title.position = "center",
main.title.size = 1.2)
tmap_arrange(hclust.map, shclust.map,
asp=NA, ncol=2)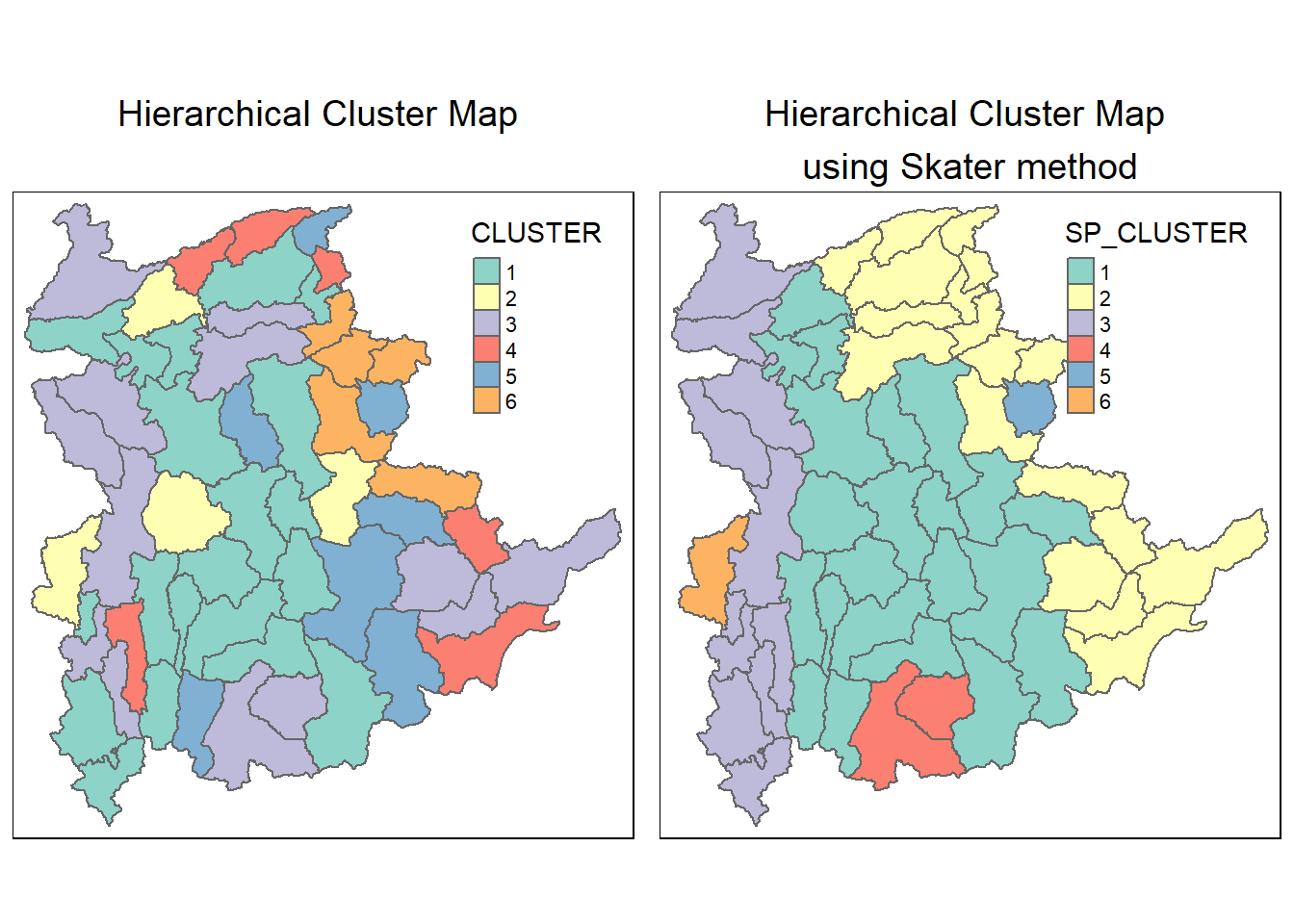
5.9 Spatially Constrained Clustering: ClustGeo Method
In this section, you will gain hands-on experience on using functions provided by ClustGeo package to perform non-spatially constrained hierarchical cluster analysis and spatially constrained cluster analysis.
| A note on ClustGeo Package |
|---|
ClustGeo package is an R package specially designed to support the need of performing spatially constrained cluster analysis. More specifically, it provides a Ward-like hierarchical clustering algorithm called In the nutshell, the algorithm uses two dissimilarity matrices D0 and D1 along with a mixing parameter alpha, whereby the value of alpha must be a real number between [0, 1]. D0 can be non-Euclidean and the weights of the observations can be non-uniform. It gives the dissimilarities in the attribute/clustering variable space. D1, on the other hand, gives the dissimilarities in the constraint space. The criterion minimised at each stage is a convex combination of the homogeneity criterion calculated with D0 and the homogeneity criterion calculated with D1. The idea is then to determine a value of alpha which increases the spatial contiguity without deteriorating too much the quality of the solution based on the variables of interest. This need is supported by a function called |
5.9.1 Ward-like hierarchical clustering: ClustGeo
ClustGeo package provides function called hclustgeo() to perform a typical Ward-like hierarchical clustering just like hclust() you learned in previous section. This only works with the Ward method.
To perform non-spatially constrained hierarchical clustering, we only need to provide the function a dissimilarity matrix as shown in the code chunk below.
nongeo_cluster <- hclustgeo(proxmat)
plot(nongeo_cluster, cex = 0.5)
rect.hclust(nongeo_cluster,
k = 6,
border = 2:5)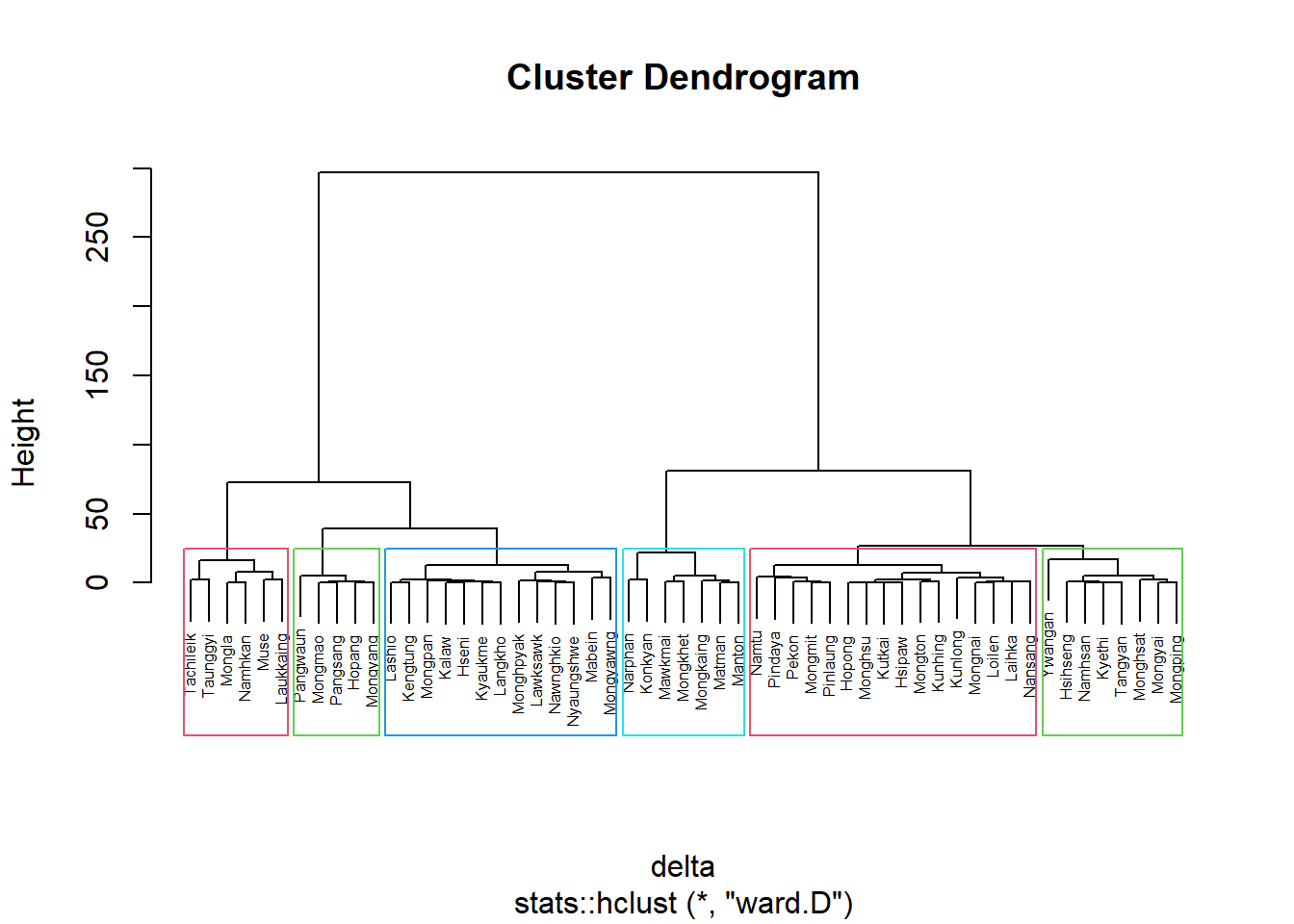
Note that the dissimilarity matrix must be an object of class dist, i.e. an object obtained with the function dist(). For sample code chunk, please refer to 5.7.3 Computing proximity matrix
5.9.1.1 Mapping the clusters formed
Similarly, we can plot the clusters on a categorical area shaded map by using the steps we learned in 5.7.9 Mapping the clusters formed.
groups <- as.factor(cutree(nongeo_cluster, k=6))shan_sf_ngeo_cluster <- cbind(shan_sf_joined, as.matrix(groups)) %>%
rename(`CLUSTER` = `as.matrix.groups.`)qtm(shan_sf_ngeo_cluster, "CLUSTER") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "ClustGeo Cluster Map",
main.title.position = "center",
main.title.size = 1.2) 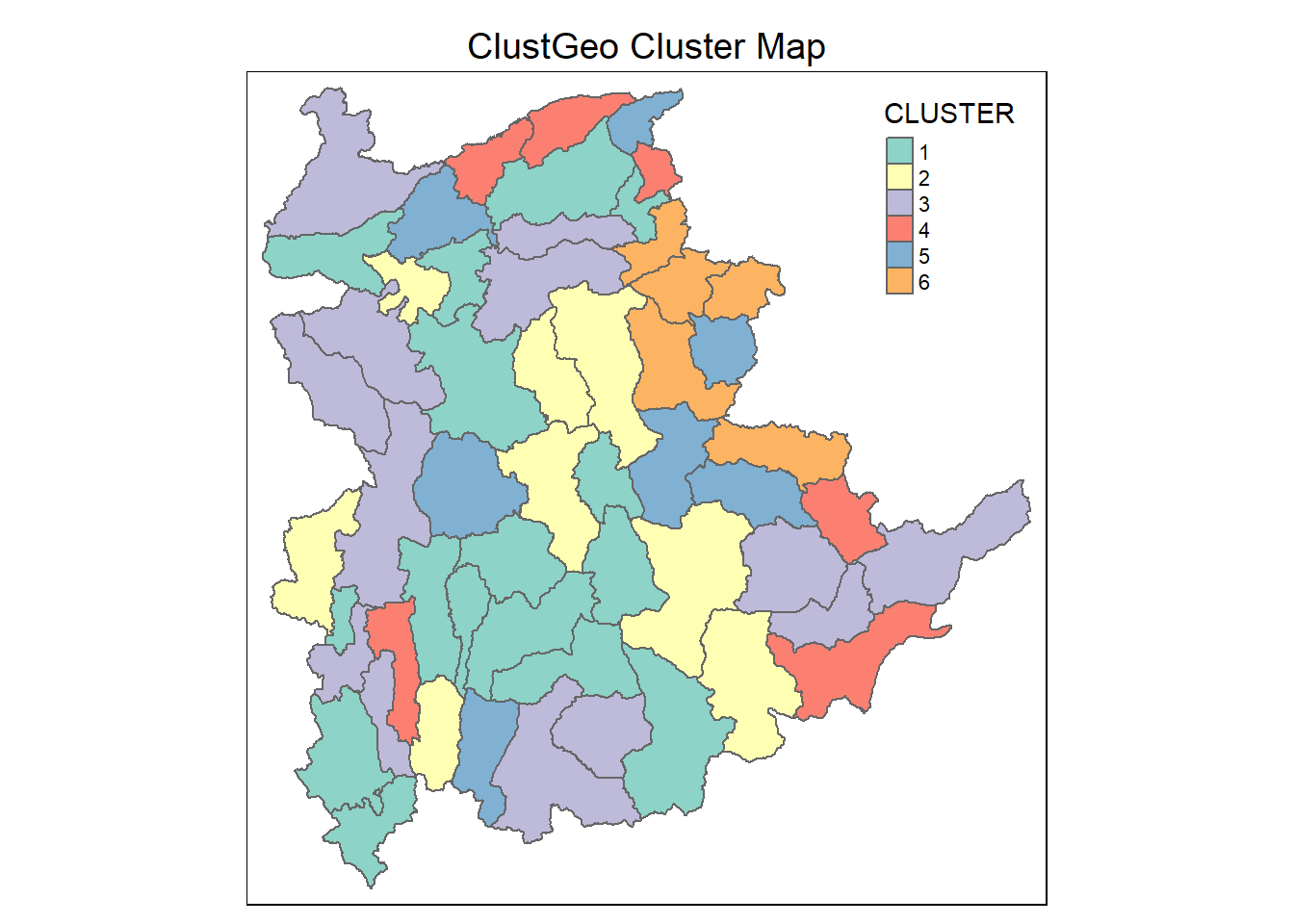
5.9.2 Spatially Constrained Hierarchical Clustering
Before we can performed spatially constrained hierarchical clustering, a spatial distance matrix will be derived by using st_distance() of sf package.
dist <- st_distance(shan_sf, shan_sf)
distmat <- as.dist(dist)Notice that as.dist() is used to convert the data frame into matrix.
Next, choicealpha() will be used to determine a suitable value for the mixing parameter alpha as shown in the code chunk below.
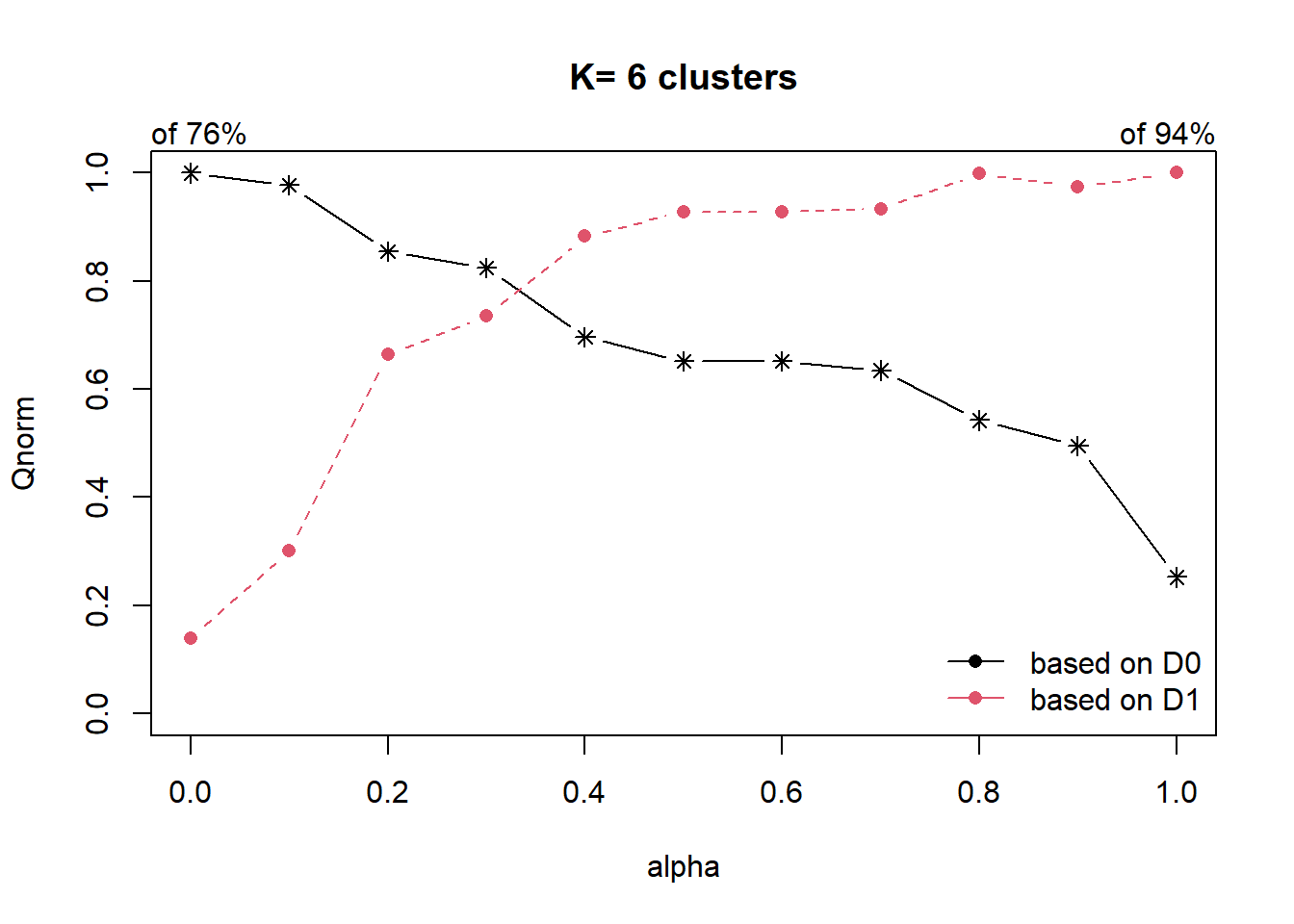
cr <- choicealpha(proxmat, distmat, range.alpha = seq(0, 1, 0.1), K=6, graph = TRUE)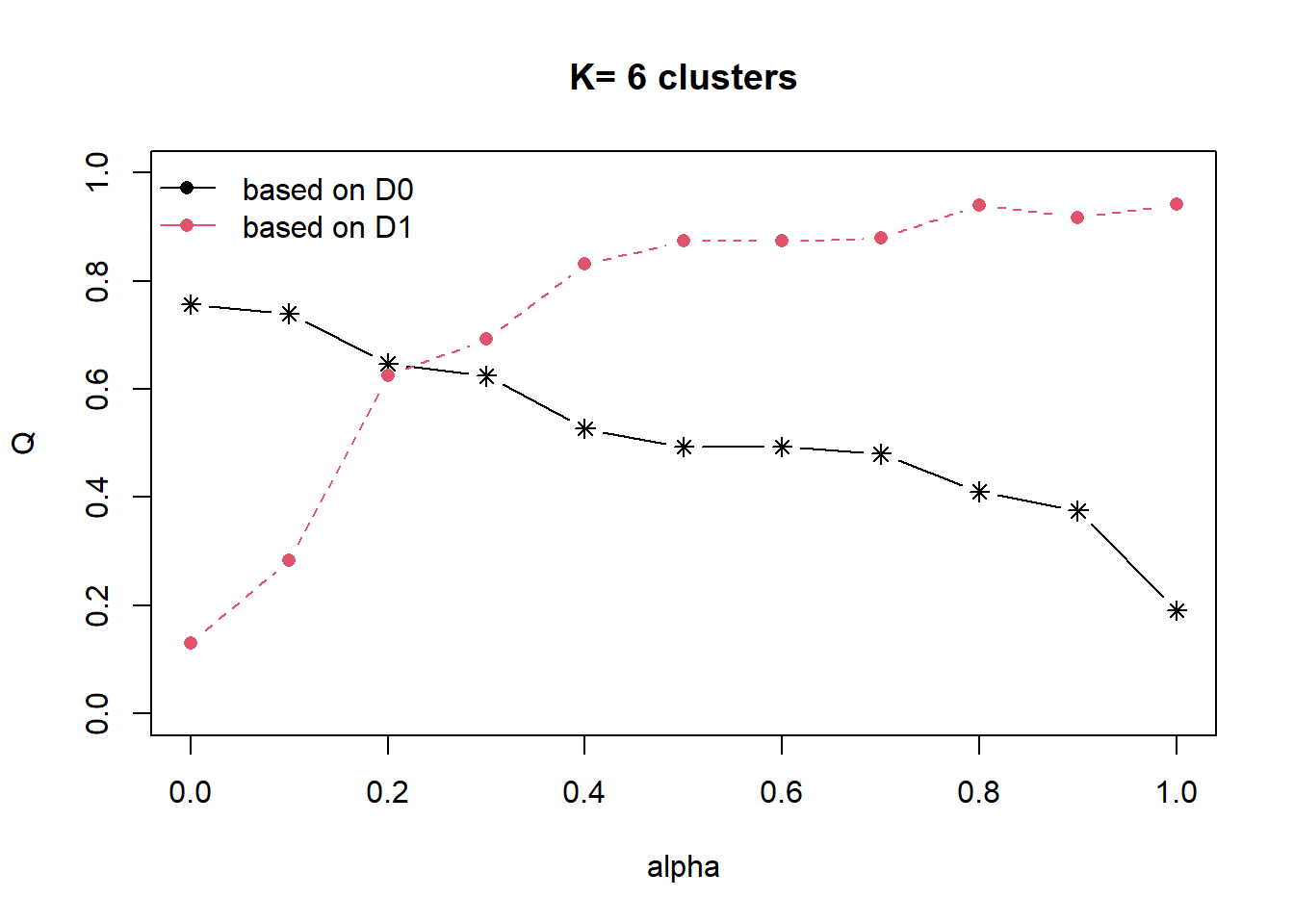
# the 0.1 in the range.alpha argument indicates that the break points should be at 0.1 interval
# To note that the argument name for number of clusters in in capital K
# graph = True is to plot the 2 graphs belowWith reference to the graphs above, alpha = 0.3 will be used as shown in the code chunk below. This is derived with reference to the Standardised Chart (with y-axis Qnorm). It shows that about 0.6 (or 60%) of the geospatial data is reflected with only a 0.2 (or 20%) reduction in aspatial data.
clustG <- hclustgeo(proxmat, distmat, alpha = 0.3)Next, cutree() is used to derive the cluster objecct.
groups <- as.factor(cutree(clustG, k=6))We will then join back the group list with shan_sf polygon feature data frame by using the code chun below.
shan_sf_Gcluster <- cbind(shan_sf_joined, as.matrix(groups)) %>%
rename(`CLUSTER` = `as.matrix.groups.`)We can now plot the map of the newly delineated spatially constrained clusters.
qtm(shan_sf_Gcluster, "CLUSTER") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "ClustGeo Cluster Map \n(alpha = 0.3)",
main.title.position = "center",
main.title.size = 1.2) 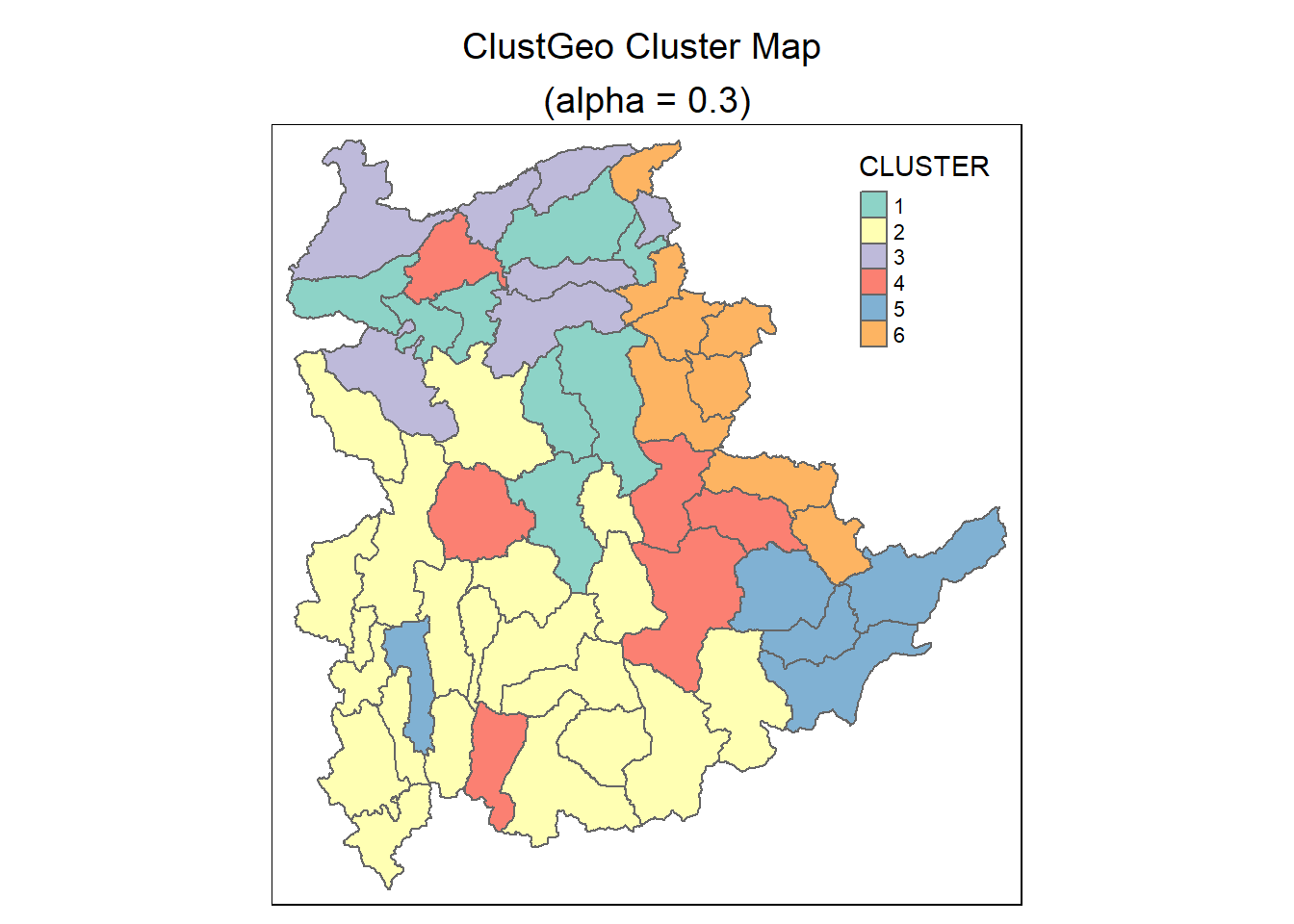
5.10 Visual Interpretation of Clusters
5.10.1 Visualise individual clustering variable
THe Code chunk below is used to check the distribution of the variable (i.e RADIO_PR) by cluster.
ggplot(data = shan_sf_ngeo_cluster,
aes(x = CLUSTER, y = RADIO_PR)) +
geom_boxplot()+
stat_summary(geom = "point",
fun.y="mean",
colour ="red",
size=2) +
ggtitle("Distribution of RADIO_PR by Cluser")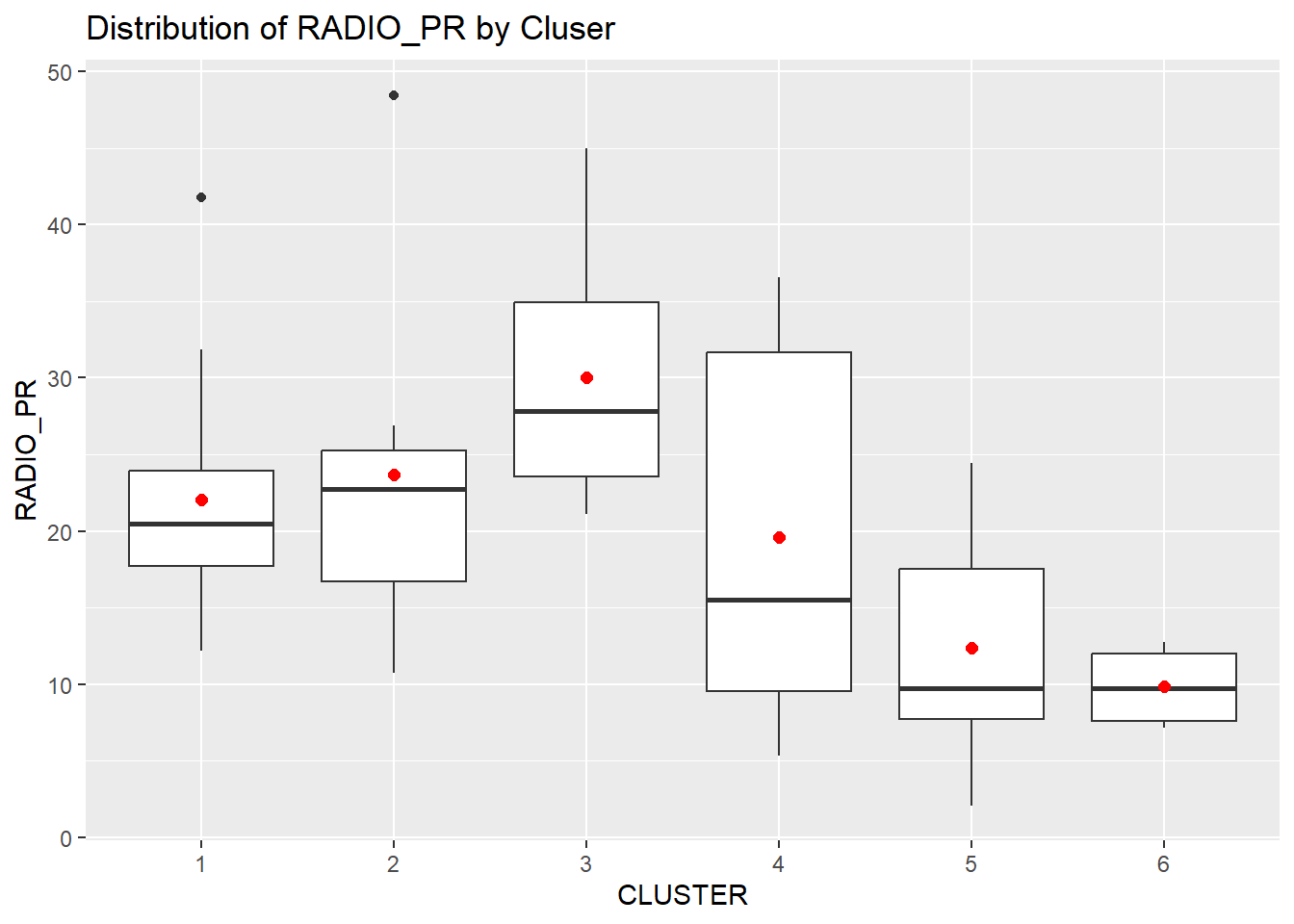
The boxplot shows that Cluster 3 displays the highest mean (red dot) Radio Ownership Per Thousand Household. This is followed by Cluster 2, 1, 4, 5 and 6.
5.10.2 Multivariate Visualisation
Past studies shown that parallel coordinate plot can be used to reveal clustering variables by cluster very effectively. In the code chunk below, ggparcoord() of GGally package.
ggparcoord(data = shan_sf_ngeo_cluster,
columns = c(17:21),
scale = "globalminmax",
alphaLines = 0.2,
boxplot = TRUE,
title = "Multiple Parallel Coordinates Plots of ICT Variables by Cluster") +
facet_grid(~ CLUSTER) +
theme(axis.text.x = element_text(angle = 90))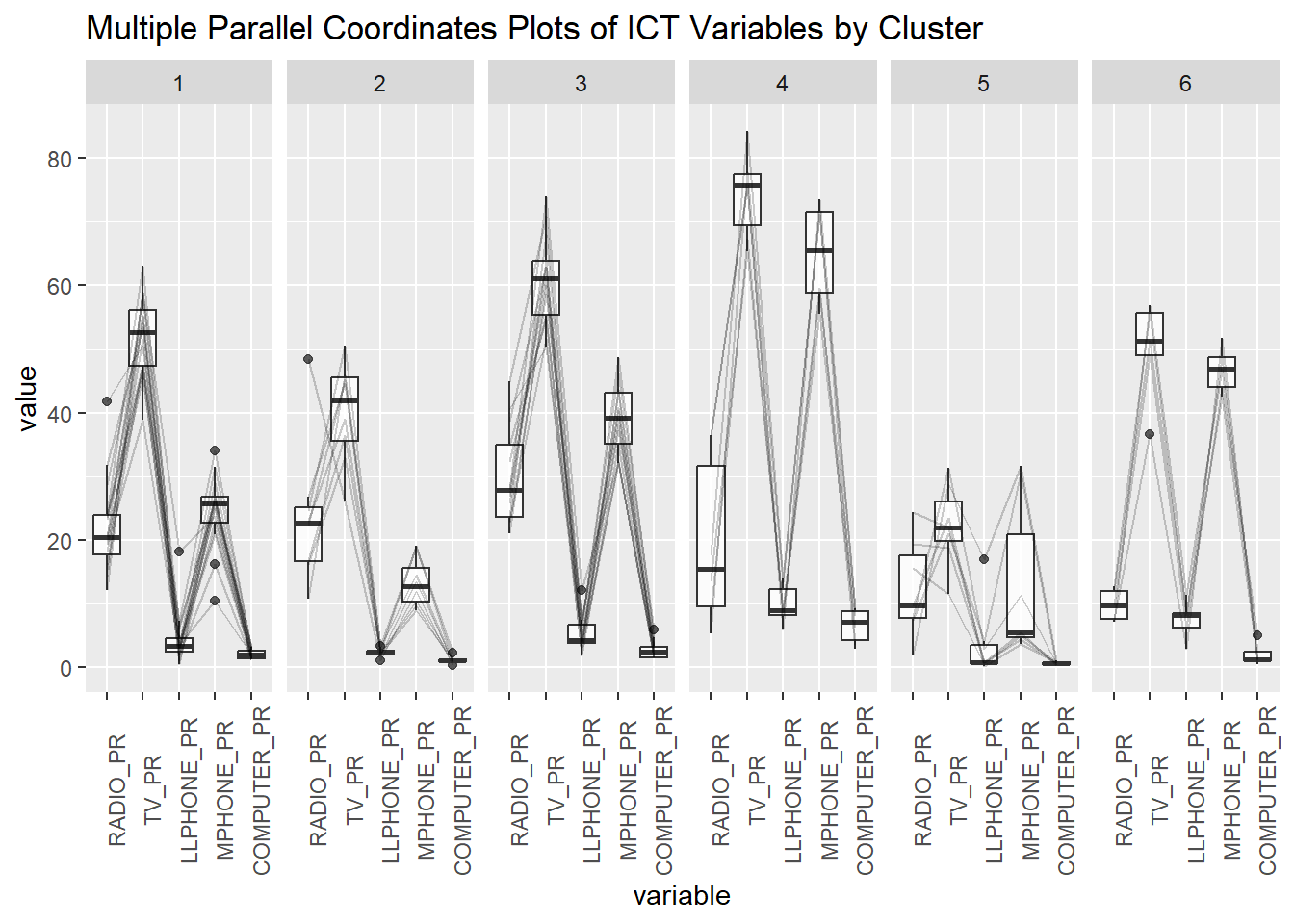
The parallel coordinate plot above shows that households in Cluster 4 townships tend to own the highest number of TV and mobile-phone. On the other hand, households in Cluster 5 tends to own the lowest of all the five ICT.
Note that the scale argument of ggparcoor() provide several methods to scale the clustering variables. They are:
std: univariately, subtract mean and divide by standard deviation.
robust: univariately, subtract median and divide by median absolute deviation.
uniminmax: univariately, scale so the minimum of the variable is zero, and the maximum is one.
globalminmax: no scaling is done; the range of the graphs is defined by the global minimum and the global maximum.
center: use uniminmax to standardize vertical height, then center each variable at a value specified by the scaleSummary param.
centerObs: use uniminmax to standardize vertical height, then center each variable at the value of the observation specified by the centerObsID param
There is no one best scaling method to use. We should explore them and select the one that best meet our analysis need.
Last but not least, we can also compute the summary statistics such as mean, median, sd, etc to complement the visual interpretation.
In the code chunk below, group_by() and summarise() of dplyr are used to derive mean values of the clustering variables.
shan_sf_ngeo_cluster %>%
st_set_geometry(NULL) %>%
group_by(CLUSTER) %>%
summarise(mean_RADIO_PR = mean(RADIO_PR),
mean_TV_PR = mean(TV_PR),
mean_LLPHONE_PR = mean(LLPHONE_PR),
mean_MPHONE_PR = mean(MPHONE_PR),
mean_COMPUTER_PR = mean(COMPUTER_PR))# A tibble: 6 × 6
CLUSTER mean_RADIO_PR mean_TV_PR mean_LLPHONE_PR mean_MPHONE_PR mean_COMPUTE…¹
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 22.1 52.1 4.42 24.6 2.05
2 2 23.7 40.2 2.39 13.4 1.15
3 3 30.0 61.1 5.22 39.2 2.90
4 4 19.6 74.4 9.90 65.1 6.55
5 5 12.4 22.4 3.80 13.2 0.668
6 6 9.86 49.9 7.45 46.8 2.10
# … with abbreviated variable name ¹mean_COMPUTER_PR